Class 9 FRANK Solutions Maths Chapter 11 - Triangles and their congruency
Learn to use the exterior angle property confidently in your exam with the help of TopperLearning’s Frank Solutions for ICSE Class 9 Mathematics Chapter 11 Triangles and their Congruency. Revise the steps to use the Angle-Side-Angle criteria or Side-Angle Side criteria with our model answers.
Also, practise the proofs given in our ICSE Class 9 Math Frank textbook solutions to understand how to explain the relation between two triangles or two line segments. In addition, grasp how to solve questions related to congruent triangles in this chapter. Further, for Maths self-study, watch our videos by experts and then evaluate your exam-preparedness with our online practice tests.
Triangles and their congruency Exercise Ex. 11.1
Solution 1

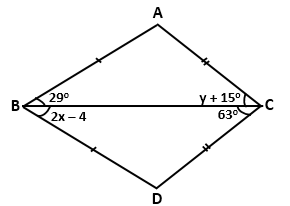
Solution 2

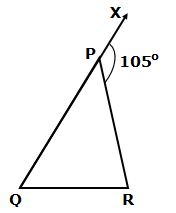
Solution 3
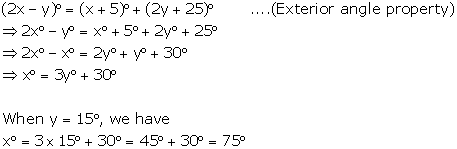
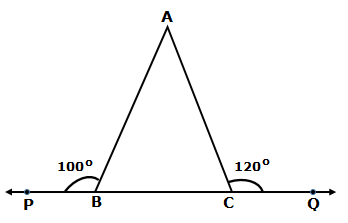
Solution 4
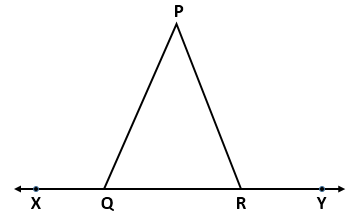

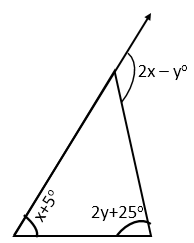
Solution 5
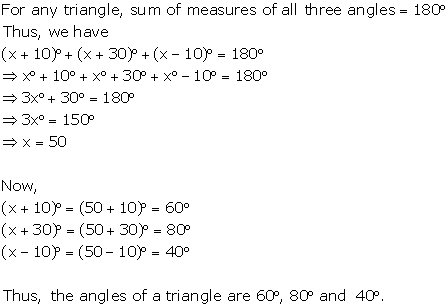
Solution 6
SR is produced to meet PQ at E.
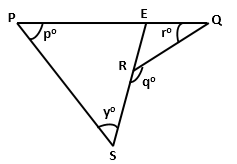

Solution 7

Solution 8
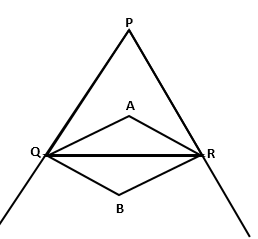


Solution 9

Solution 10
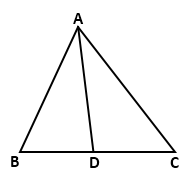
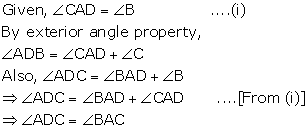
Solution 11
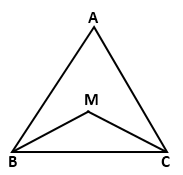

Solution 12
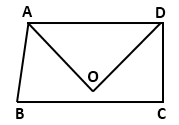

Solution 13

Solution 14
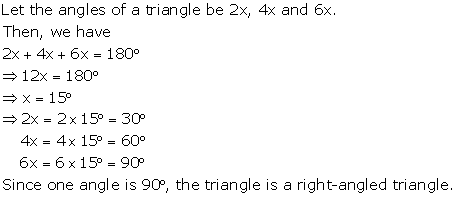
Solution 15
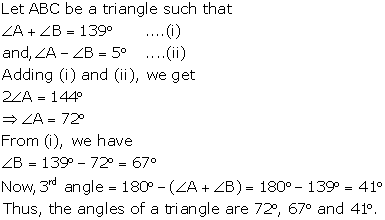
Solution 16
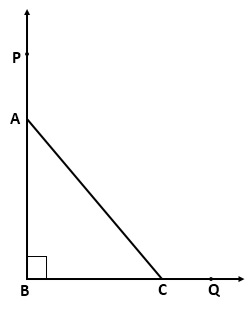

Triangles and their congruency Exercise Ex. 11.2
Solution 1
Solution 5
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 17
Solution 19
Solution 20
Solution 21
Solution 23
Solution 24
Solution 25
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
Solution 31
Solution 2
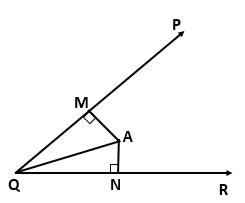

Solution 3

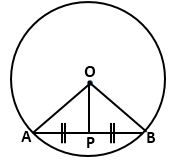

Solution 4



Solution 6
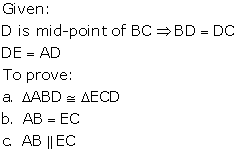
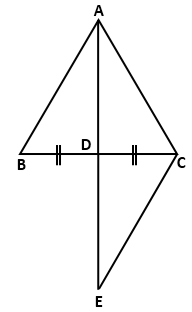

Solution 16

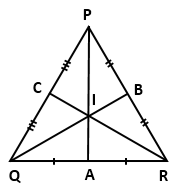

Solution 18

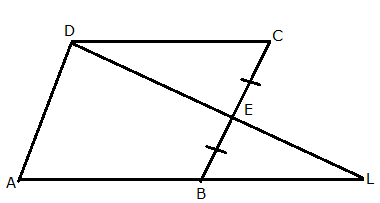

Solution 32