Class 9 FRANK Solutions Maths Chapter 18 - Rectilinear Figures
Understand polygons with Frank Solutions for ICSE Class 9 Mathematics Chapter 18 Rectilinear Figures. Learn to use the correct theorems for calculating the sum of interior angles of a polygon or sum of exterior angles of a polygon. Also, practise how to calculate the measurement of each angle of a polygon with our chapter solutions.
Revising the Frank textbook solutions for ICSE Class 9 Maths can help you to brush up the concepts on how to find the number of sides of a given polygon. Further, if you have any doubts related to rectilinear figures, visit the ‘UnDoubt’ platform at TopperLearning for answers from experts.
Ex. 18.1
Rectilinear Figures Exercise Ex. 18.1
Solution 16(a)

Solution 16(b)

Solution 17(a)

Solution 17(b)

Solution 18

Solution 19
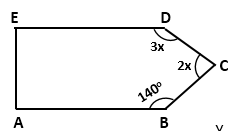
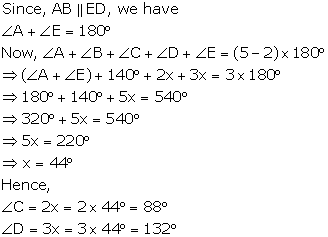
Solution 20

Solution 21

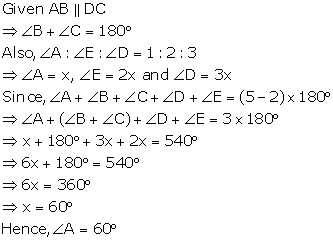
Solution 22
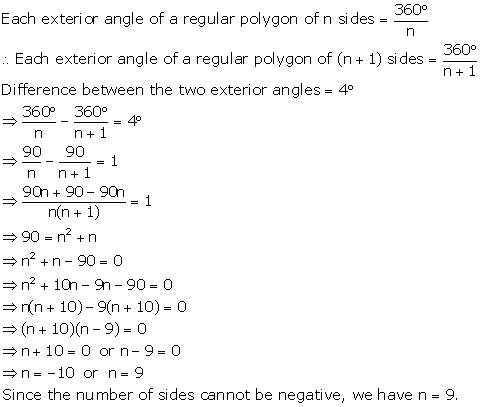
Solution 23

Solution 33
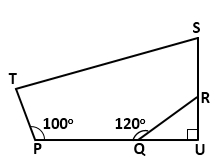

Solution 34

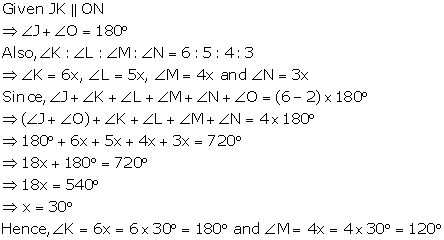
Solution 35
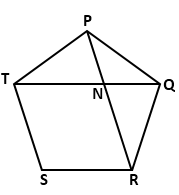

Solution 36
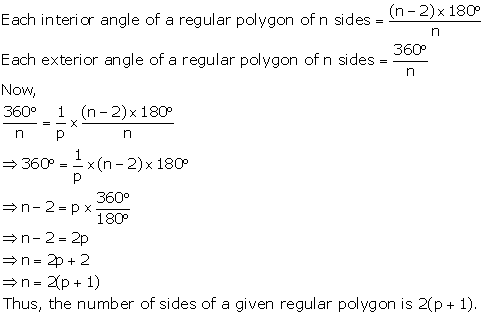
Solution 37

Solution 1

Solution 2

Solution 3

Solution 4

Solution 5

Solution 6

Solution 7

Solution 8

Solution 9

Solution 10

Solution 11

Solution 12

Solution 13

Solution 14

Solution 15

Solution 24
Solution 25
Solution 26
Solution 27
Solution 28
Solution 29
Solution 30
Solution 31
Solution 32










