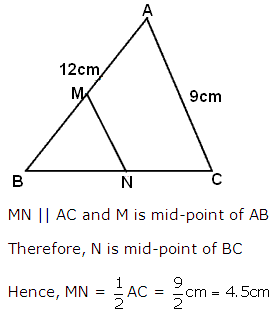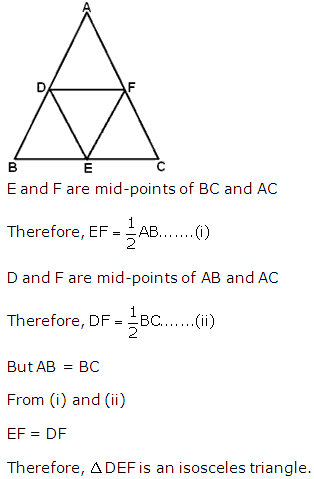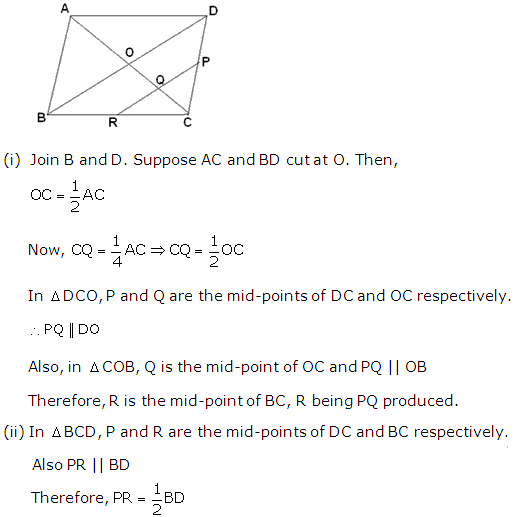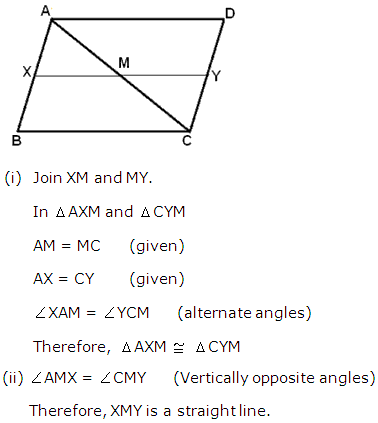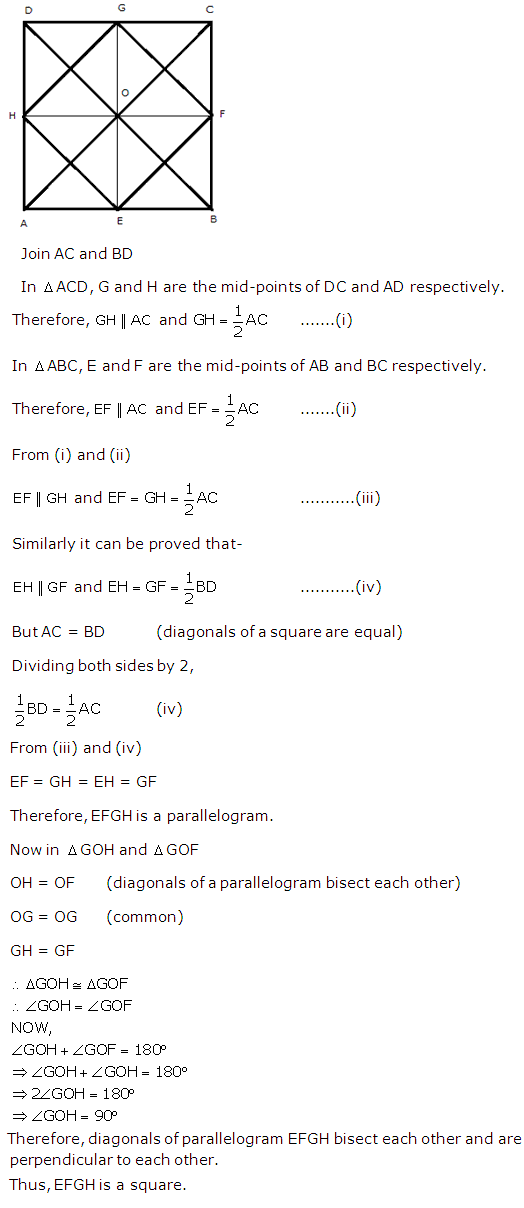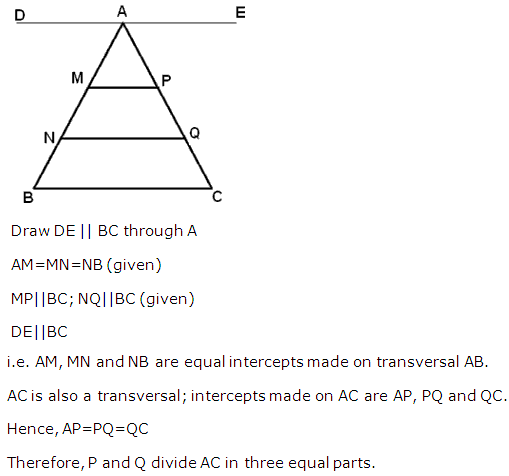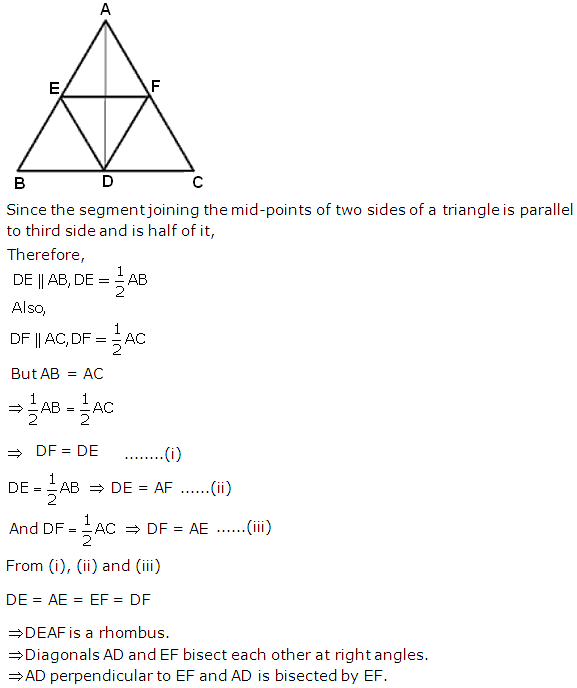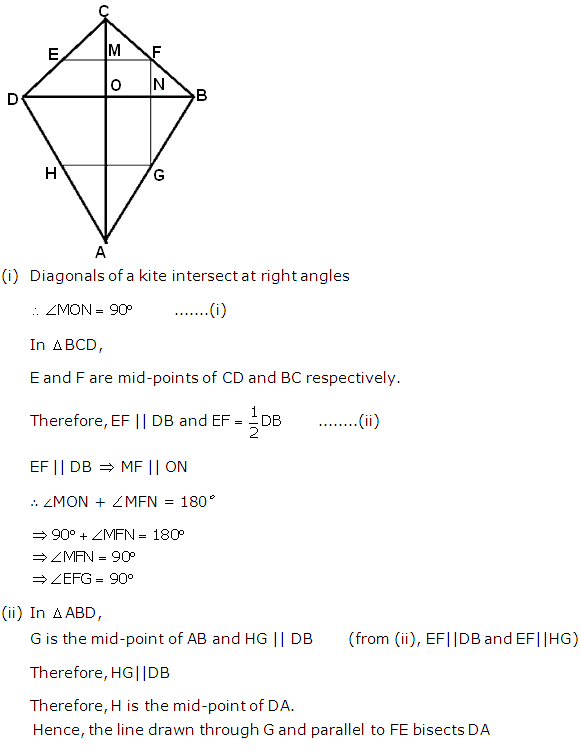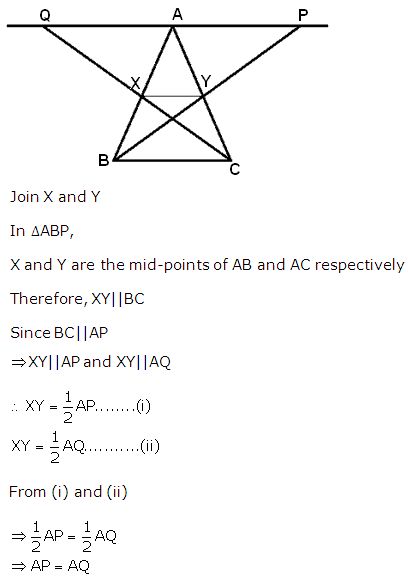Class 9 FRANK Solutions Maths Chapter 15 - Mid-point and Intercept Theorems
Practise Frank Solutions for ICSE Class 9 Mathematics Chapter 15 Mid-point and intercept theorems at TopperLearning. If you find questions on working with the mid-point of sides of a triangle mind-boggling, our reference solutions will help you. Whether it is sides of a rhombus or a parallelogram, you can check the steps that experts will use to solve Maths problems.
Revise textbook questions on the Mid-point theorem and Intercept theorem effectively with Frank textbook solutions. For more ICSE Class 9 Maths resources, explore our Selina solutions, online practice tests, videos and more.
Mid-point and Intercept Theorems Exercise Ex. 15.1
Solution 3(a)
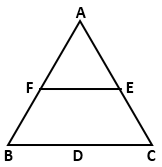

Solution 3(b)
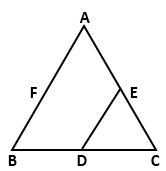

Solution 3(c)
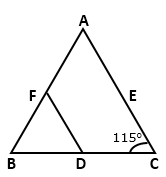
![]()
Solution 5
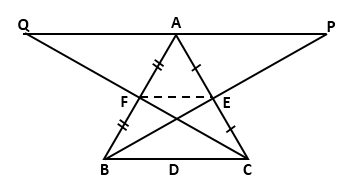

Solution 11
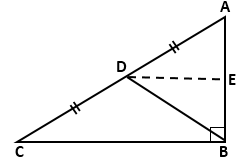

Solution 15(a)
Let us draw a diagonal AC which meets PQ at O as shown below:
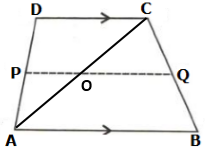



Solution 18
Construction: Draw DS ∥ BF, meeting AC at S.


Solution 24



Solution 1

Solution 2
Solution 4

Solution 6
Solution 7
Solution 8
Solution 9
Solution 10
Solution 12
Solution 13
Solution 14
Solution 16
Solution 17
Solution 19
Solution 20
Solution 21
Solution 22
Solution 23
Mid-point and Intercept Theorems Exercise Ex. 15.2
Solution 1
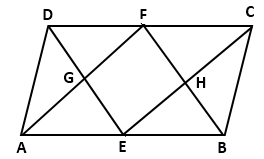


Solution 2
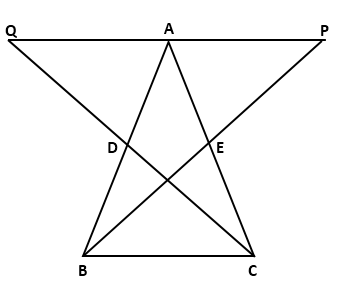

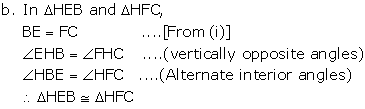
Solution 3
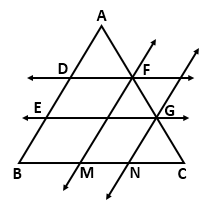

Solution 4

Solution 5
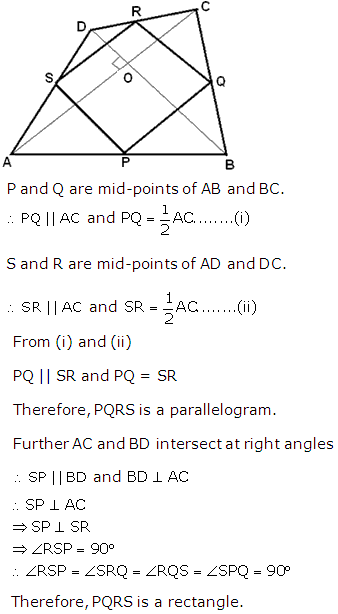
The figure is as below:
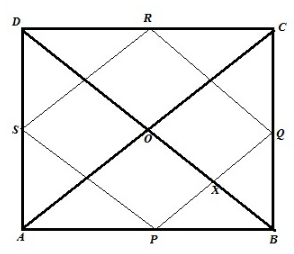
Let ABCD be a quadrilateral where P, Q, R, S are the midpoints of sides AB, BC, CD, DA respectively.
Diagonals AC and BD intersect at right angles at point O. We need to show that PQRS is a rectangle

Solution 6
Note: This question is incomplete.
According to the information given in the question,
F could be any point on BC as shown below:
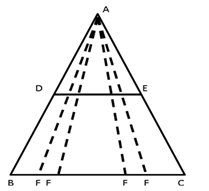
So, this makes it impossible to prove that DP = DE, since P too would shift as F shift because P too would be any point on DE as F is.
Note: If we are given F to be the mid-point of BC, the result can be proved.
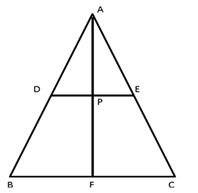

Solution 7

From the figure EF ∥ AB and E is the midpoint of BC.
Therefore, F is the midpoint of AC.
Here EF ∥ BD, EF = BD as D is the midpoint of AB.
BE ∥ DF, BE = DF as E is the midpoint of BC.
Therefore BEFD is a parallelogram.
Remark: Figure modified
Solution 8
![]()

Solution 9