FRANK Solutions for Class 9 Maths Chapter 1 - Irrational Numbers

In the Frank Solutions for ICSE Class 9 Mathematics Chapter 1 Irrational Numbers, understand the steps to place the given rational numbers in the ascending order. Find out how to determine whether the given number is rational or irrational.

Also, practise simplifying the given expression by using the technique of rationalising the denominator. Learn all this and more through TopperLearning’s Frank textbook solutions. To ensure a good grasp of irrational numbers, explore ICSE Class 9 Maths resources like videos, practice question papers and more.

Read  more
Page / Exercise

Chapter 1 - Irrational Numbers Ex. 1.1

Solution 1(a)

Solution 1(b)

Solution 1(c)

Solution 1(d)

Solution 1(e)

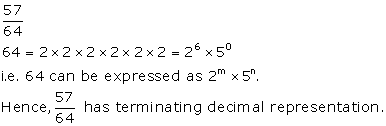
Solution 1(f)

Solution 1(g)

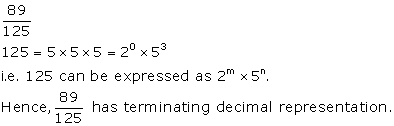
Solution 1(h)

Solution 1(i)

Solution 2(a)

Solution 2(b)

Solution 2(c)

Solution 2(d)

Solution 3

(vi)

begin mathsize 12px style 2 over 3 equals 0.6666....... equals 0.6 with dot on top end style

Solution 4(a)

Solution 4(b)

Solution 4(c)

Solution 4(d)

Solution 4(e)

Solution 4(f)

Solution 4(g)

Solution 4(h)

Solution 4(i)

Solution 5(b)

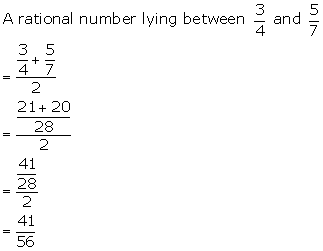
Solution 5(c)

Solution 5(d)

Solution 5(a)

Solution 6(a)

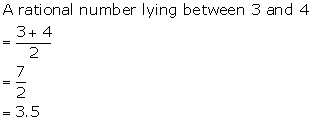
Solution 6(b)

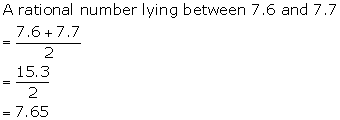
Solution 6(c)

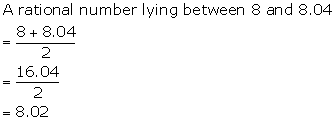
Solution 6(d)

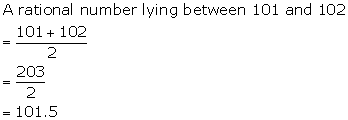
Solution 7(a)

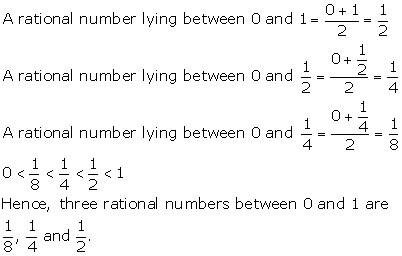
Solution 7(b)

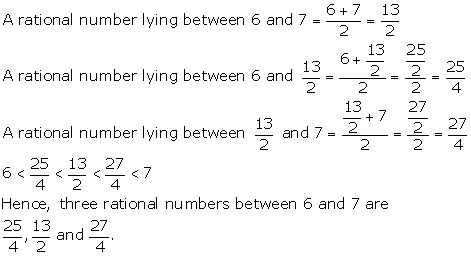
Solution 7(c)

Solution 7(d)

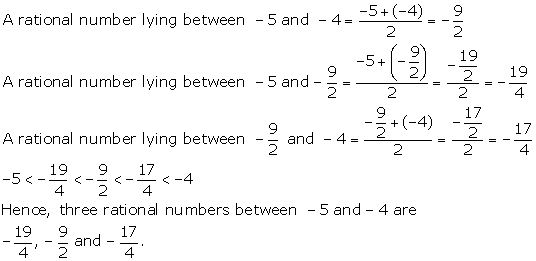
Solution 8(a)

Solution 8(b)

Solution 9(a)

Solution 9(b)

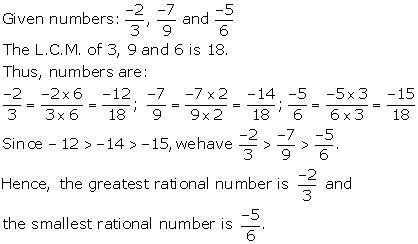
Solution 10(a)

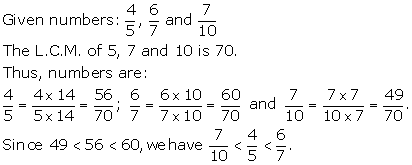
Solution 10(b)

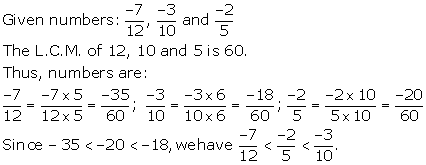
Solution 10(c)

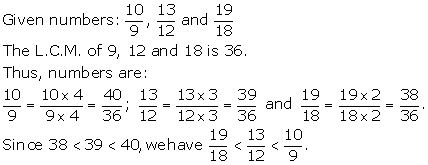
Solution 10(d)

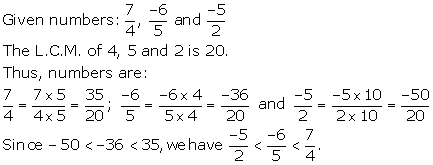
Solution 11(a)

Solution 11(b)

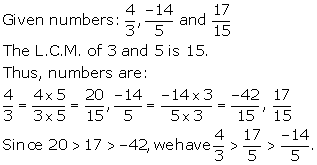
Solution 11(c)

Solution 11(d)

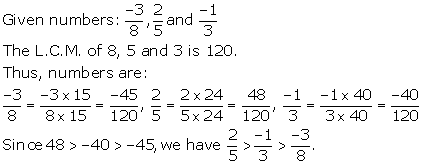
Solution 12(a)

Solution 12(b)

Solution 12(c)

Solution 12(d)

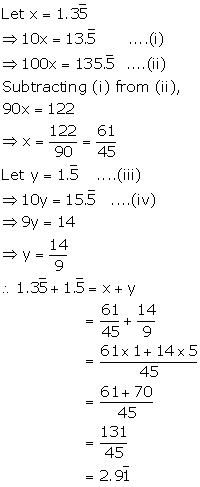
Chapter 1 - Irrational Numbers Ex. 1.2

Solution 1(a)

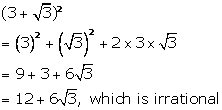
Solution 1(b)

Solution 1(c)

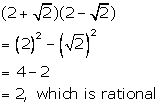
Solution 1(d)

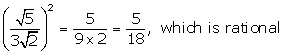
Solution 2(a)

Solution 2(b)

 

Solution 2(c)

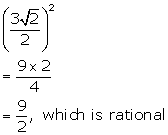
Solution 2(d)

Solution 3

Solution 4

Solution 5(a)

Solution 5(b)

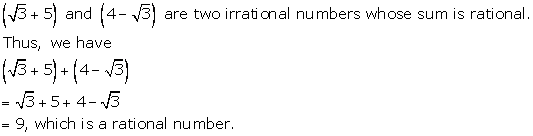
Solution 5(c)

Solution 5(d)

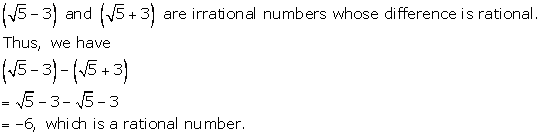
Solution 5(e)

Solution 5(f)

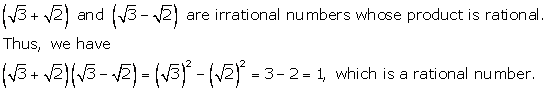
Solution 6(a)

Solution 6(b)

Solution 7(a)

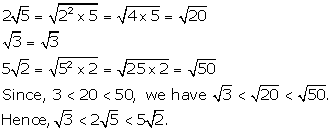
Solution 7(b)

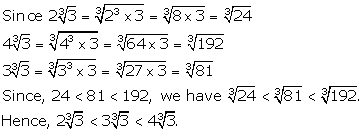
Solution 7(c)

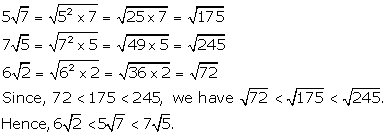
Solution 7(d)

Solution 8(a)

Solution 8(b)

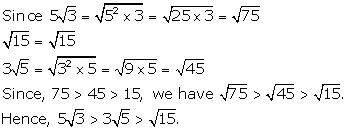
Solution 8(c)

Solution 9

Solution 10

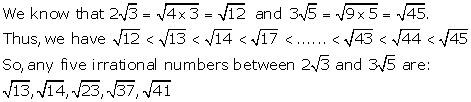
Solution 11

Solution 12

Solution 13(a)

 

Solution 13(b)

Solution 13(c)

Solution 13(d)

Solution 13(e)

Solution 13(f)

Solution 14

 

 

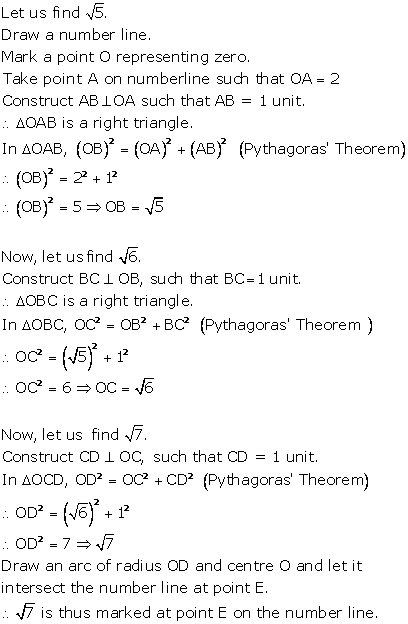
Chapter 1 - Irrational Numbers Ex. 1.3

Solution 1(a)

Solution 1(b)

Solution 1(c)

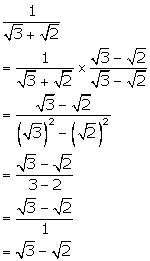
Solution 1(d)

Solution 1(e)

Solution 1(f)

Solution 1(g)

Solution 1(h)

Solution 1(i)

Solution 2

Solution 3
Solution 4

Solution 5

Solution 6(a)

Solution 6(b)

Solution 6(c)

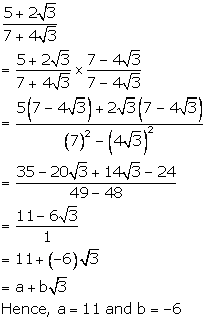
Solution 6(d)

Solution 6(e)

Solution 6(f)

Solution 6(g)

Solution 6(h)

Solution 6(i)

Solution 6(j)

Solution 7

(iv)

Solution 8

(v)

Solution 9

Solution 10

Solution 11