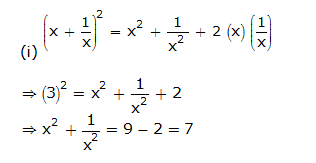Class 9 FRANK Solutions Maths Chapter 4 - Expansions
Learn to expand the given mathematical expressions with Frank Solutions for ICSE Class 9 Mathematics Chapter 4 Expansions. Practise the solutions to evaluate expressions without using the multiplication method. Also, revise the steps to find the cube of the given expression with the help of our chapter solutions.
Also, practise the Frank textbook solutions to relearn the methods for solving expansions-based problems. You can also solve related problems by accessing TopperLearning’s online sample question papers and previous years’ papers with solutions. And if you have trouble with difficult questions, get a response to your doubts on our ‘UnDoubt’ section.
Ex. 4.1
Ex. 4.2
Expansions Exercise Ex. 4.1
Solution 1



(V)
Solution 2
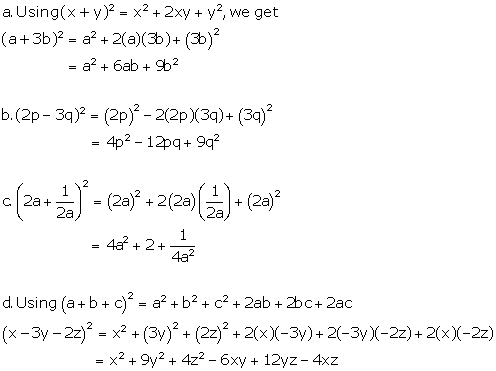
Solution 3
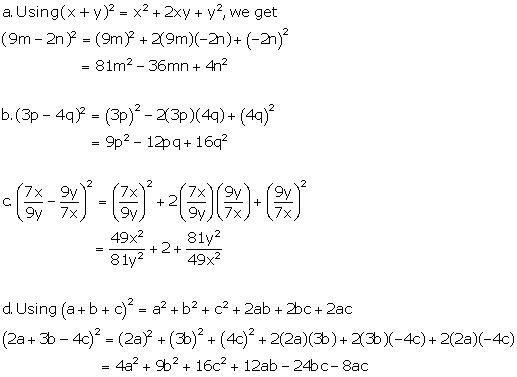
Solution 4

Solution 5
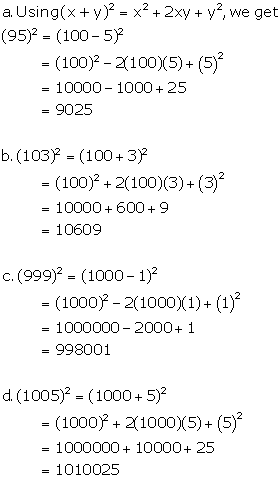
Solution 6

Solution 7

Solution 8

Solution 9
Solution 10
Solution 11

Solution 12
Solution 13
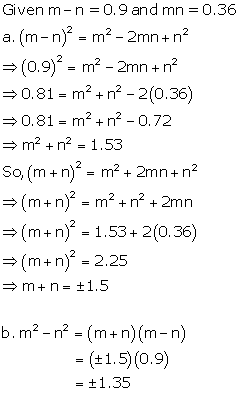
Solution 14
Solution 15
Solution 16
Solution 17
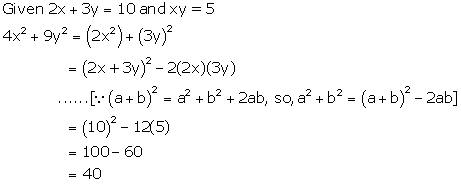
Solution 18
Solution 19
Solution 20
Solution 21
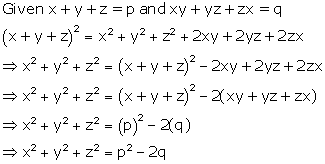
Expansions Exercise Ex. 4.2
Solution 1




(v)

Solution 2

Solution 3

Solution 4
Solution 5
Solution 6(a)
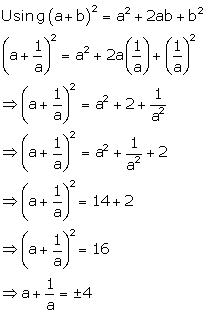
Solution 6(b)
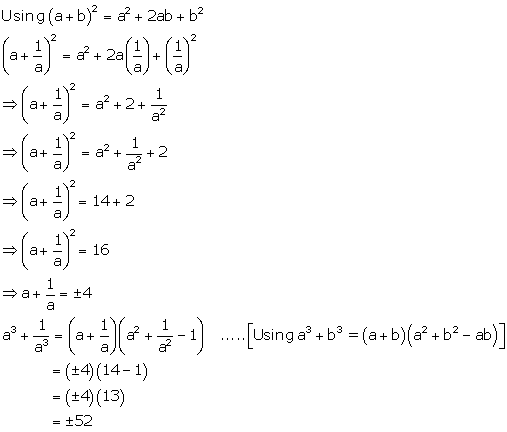
Solution 7
Solution 8
Solution 9
Solution 10
Solution 11
Solution 12
Solution 13
Solution 14
Solution 15
Solution 16
Solution 17
Solution 18
Solution 19
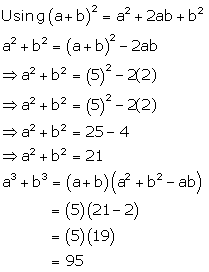
Solution 20
Solution 21
Solution 22
Solution 23
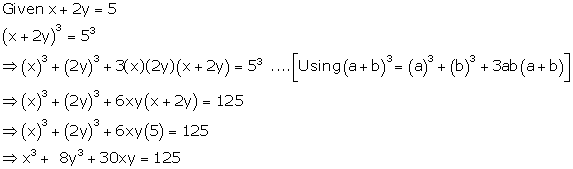
Solution 24(a)
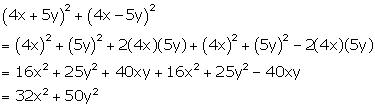
Solution 24(b)
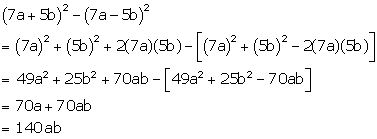
Solution 24(c)

Solution 24(d)
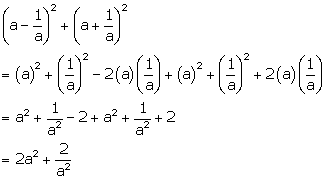
Solution 24(e)
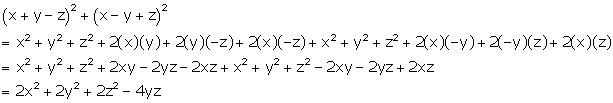
Solution 24(f)
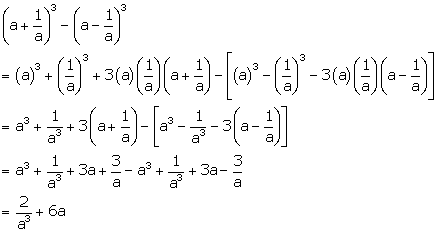
Solution 24(g)
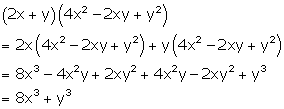
Solution 24(h)
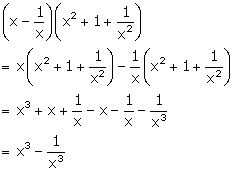
Solution 24(i)
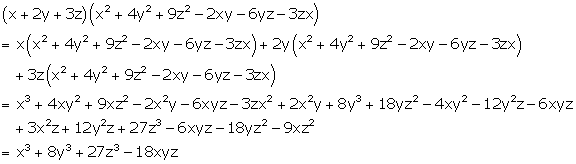
Solution 24(j)
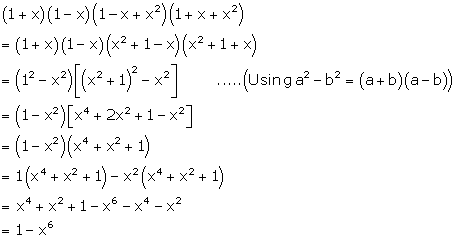
Solution 24(k)
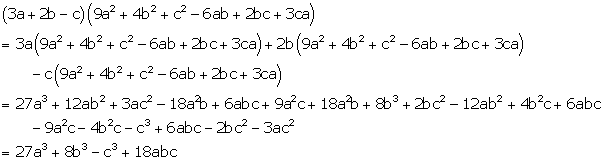
Solution 24(l)

Solution 24(m)
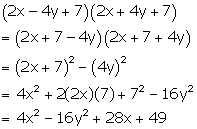
Solution 24(n)
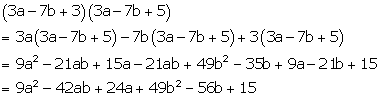
Solution 24(o)

Solution 25