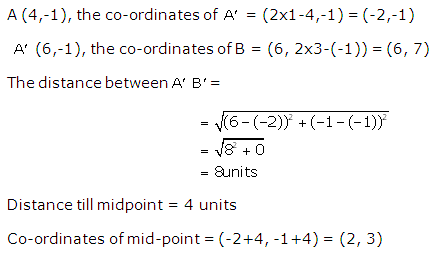Class 10 FRANK Solutions Maths Chapter 8 - Reflection
Revise Maths lessons with Frank Solutions for ICSE Class 10 Mathematics Chapter 8 Reflection at TopperLearning. Practise Maths problems to relearn the steps to find the distance between the points of reflection based on the given data. Understand how to find the coordinates of a mirror image of the given points with the expert answers available on our study portal.
You can work towards increasing your Maths score in the board exam with thorough Maths practice. To support you, we have made available learning resources like ICSE Class 10 Maths practice tests, sample mock exam papers and more.
Ex. 8.1
Reflection Exercise Ex. 8.1
Solution 1
(i) (3,-9)
The co-ordinate of the given point under reflection in the x-axis is: (3,9).
(ii) (-7, 5)
The co-ordinate of the given point under reflection in the x-axis is: (-7,-5).
(iii) (0, 6)
The co-ordinate of the given point under reflection in the x-axis is: (0,-6).
(iv) (-4,-8)
The co-ordinate of the given point under reflection in the x-axis is: (-4, 8).
The co-ordinate of the given point under reflection in the x-axis is: (3,9).
(ii) (-7, 5)
The co-ordinate of the given point under reflection in the x-axis is: (-7,-5).
(iii) (0, 6)
The co-ordinate of the given point under reflection in the x-axis is: (0,-6).
(iv) (-4,-8)
The co-ordinate of the given point under reflection in the x-axis is: (-4, 8).
Solution 2
(i) (2, 8)
The co-ordinate of the given point under reflection in the y-axis is: (-2,8).
(ii) (-1,-3)
The co-ordinate of the given point under reflection in the y-axis is: (1,-3).
(iii) (5,-6)
The co-ordinate of the given point under reflection in the y-axis is: (-5,-6).
(iv) (-4, 7)
The co-ordinate of the given point under reflection in the y-axis is: (4, 7).
The co-ordinate of the given point under reflection in the y-axis is: (-2,8).
(ii) (-1,-3)
The co-ordinate of the given point under reflection in the y-axis is: (1,-3).
(iii) (5,-6)
The co-ordinate of the given point under reflection in the y-axis is: (-5,-6).
(iv) (-4, 7)
The co-ordinate of the given point under reflection in the y-axis is: (4, 7).
Solution 3
(i) (-1,-4)
The co-ordinate of the given point under reflection in the origin is: (1, 4)
(ii) (2, 7)
The co-ordinate of the given point under reflection in the origin is: (-2,-7)
(iii) (0, 2)
The co-ordinate of the given point under reflection in the origin is: (0,-2)
(iv) (9,-9)
The co-ordinate of the given point under reflection in the origin is: (-9, 9)
The co-ordinate of the given point under reflection in the origin is: (1, 4)
(ii) (2, 7)
The co-ordinate of the given point under reflection in the origin is: (-2,-7)
(iii) (0, 2)
The co-ordinate of the given point under reflection in the origin is: (0,-2)
(iv) (9,-9)
The co-ordinate of the given point under reflection in the origin is: (-9, 9)
Solution 4
P' = (2, 10). Therefore, the co-ordinates of P under reflection in the x-axis = (2,-10)
Solution 5
S= (2,-5). Therefore, the co-ordinates of S' under reflection in the origin = (-2, 5)
Solution 6
P' = (-3, 4).
Therefore, the co-ordinates of P under reflection in the x-axis = (-3,-4)
and the co-ordinates of P" under reflection in the origin = (3,-4).
The single transformation = reflection in the y-axis.
Therefore, the co-ordinates of P under reflection in the x-axis = (-3,-4)
and the co-ordinates of P" under reflection in the origin = (3,-4).
The single transformation = reflection in the y-axis.
Solution 7
P' = (8,-6).
Therefore, the co-ordinates of P under reflection in the x-axis = (8, 6)
and the co-ordinates of P" under reflection in the y-axis = (-8, 6).
Therefore, the co-ordinates of P under reflection in the x-axis = (8, 6)
and the co-ordinates of P" under reflection in the y-axis = (-8, 6).
Solution 8
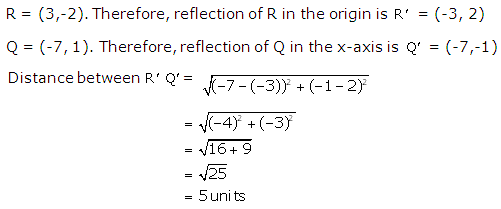
Solution 9
B = (3, 2), Therefore, reflection of B in the x-axis is B'= (3,-2)
C = (0, 3), Therefore, reflection of C in the line B is C' = (6, 3).
C = (0, 3), Therefore, reflection of C in the line B is C' = (6, 3).
Solution 10
P"= (5,-2), therefore, co-ordinates of P' = (-5, 2) and hence the coordinates of P = (-5,-2)
Single transformation = reflection in the y-axis
Single transformation = reflection in the y-axis
Solution 11
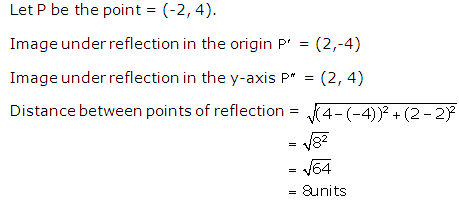
Solution 12
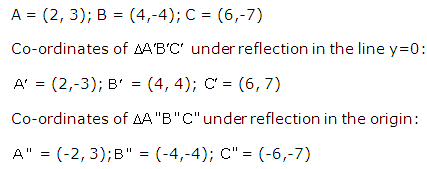
Solution 13
P = (-8, 1), therefore co-ordinates of P' under reflection in the x-axis = (-8, -1).
Hence, the co-ordinates of P" under reflection in the origin = (8, 1).
The single transformation = reflection in the y-axis.
Hence, the co-ordinates of P" under reflection in the origin = (8, 1).
The single transformation = reflection in the y-axis.
Solution 14
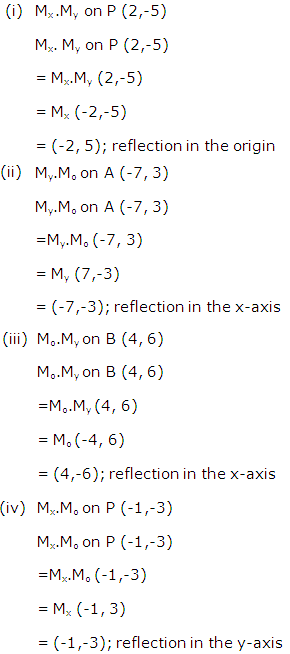
Solution 15
(i) y = 0
Co-ordinates of image = (-5, 2x0-4)= (-5,-4)
(ii) y = 4
Co-ordinates of image = (-5, 2x4-4)= (-5,4)
Co-ordinates of image = (-5, 2x0-4)= (-5,-4)
(ii) y = 4
Co-ordinates of image = (-5, 2x4-4)= (-5,4)
Solution 16
(i) x = 0
Co-ordinates of image =(2x0-4,-1)= (-4,-1)
(ii) y = 5
Co-ordinates of image = (4, 2x5-(-1)) = (4, 11)
Co-ordinates of image =(2x0-4,-1)= (-4,-1)
(ii) y = 5
Co-ordinates of image = (4, 2x5-(-1)) = (4, 11)
Solution 17
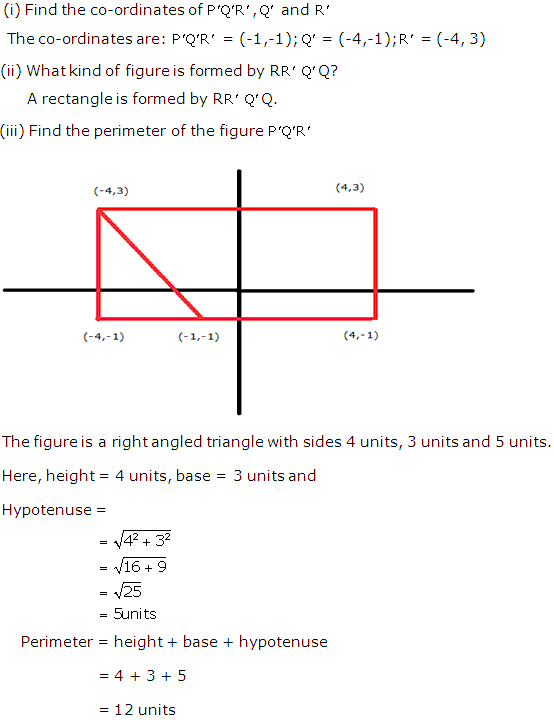
Solution 18
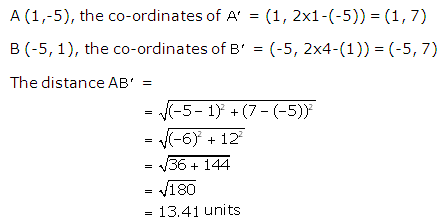
Solution 19