JEE Class main Answered
YDSE

Asked by swayamagarwal2114 | 17 Jul, 2022, 12:05: PM
Part (i)
Light ray incident on slits S1 and S2 at angle α = (1.8/π)o .
Hence additional phase Δφ2 at S2 = ( d sinα ) × ( 2π / λ )
additional phase Δφ2 at S2 calculated from above expression is
Δφ2 = 10-3 × sin (1.8/π) × [ 2π / ( 6000× 10-10 ) ] = (100/3)π
After slit S1 , there is a transparent film of thickness t and refractive index μ .
hence phase difference Δφ1 between light rays emerging from S1 and S2 is
Δφ1 = ( μ - 1 ) t × ( 2π / λ ) = (1/2) × 4 × 10-6 × [ 2π / ( 0.6 × 10-6 ) ]
Δφ1 = (20/3)π
Net phase difference = Δφ2 - Δφ1 = (80/3)π
Let Io be the intensity of light emerging from slit S1 . Thin film absorbs 50% intensity.
Hence after thin film light intensity ( Io / 2 )
Width of slit S2 is twice of that of S1 . hence light intensity from slit S2 is ( 2 Io )
when two light rays of intensities I1 and I2 are added , we get resultant intensity IR as
IR = I1 + I2 + 2 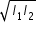 cosΔφ
cosΔφ
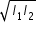 cosΔφ
cosΔφ where Δφ is the phase difference between two light rays.
---------------------------------
Part (i)
Intensity at centre point of screen = (Io/2) + 2Io + 2 [ (Io/2)(2Io) ]1/2 cos [ (80/3)π ) = (3/2) Io
Maximum intensity occurs at a point where phase difference is zero
Hence Maximum intensity = (Io/2) + 2Io + 2 [ (Io/2)(2Io) ]1/2 = (9/2) Io
If we denote maximum intensity (9/2) Io = I ,
then Intensity at centre point of screen = { [ (3/2) Io ] / [ (9/2) Io ] } × I = (1/3) I
-------------------------
Part (ii)
Minimum intensity is when phase difference Δφ = π
Mimimum intensity = (Io/2) + 2Io + 2 [ (Io/2)(2Io) ]1/2 cos [ π ] = Io/2
If we denote maximum intensity (9/2) Io = I ,
----------------------------------------
Part (iii)
Maxima of intensity occure at angular position θn , if following condition is satisfied
Δp + ( d sinθn ) = nλ
where Δp is initial phase difference at slits position.
Let yn be the vertical distance from O on screen for n-th maximum, then we have
Δp + ( d × (yn/D ) = nλ .......................... (1)
Let yn+1 be the vertical distance from O on screen for (n+1)-th maximum, then we have
Δp + ( d × (yn+1/D ) = (n+1)λ ......................(2)
By subracting eqn.(1) from eqn.(2) , we get
(d/D) [ yn+1 - yn ] = λ
Hence fringe width = [ yn+1 - yn ] = ( λ D ) /d = ( 6000 × 10-10 ) / 10-3 = 6 × 10-4 m
fringe width = 0.6 mm
-----------------------------------------------------
Part (iv)
we have seen from Part (i) ,Net phase difference at O = Δφ2 - Δφ1 = (80/3)π
Net phase difference at O = [13+ (1/3)]2π
To get phase difference as integer multiples of 2π ,
required additional phase difference = (2/3) (2π ) = (4/3)π
Hence required path difference = (4/3)π × ( λ / 2π ) = (2/3) λ
angular position θ to get this additional phase difference is determined from the following equation
d sinθ ≈ d tanθ = d × (y/D) = (2/3)λ
where y is distance of nearest maximum from O and D is slit-to-screen distance
y = [ (2/3) × 6000 × 10-10 ] / ( 10-3 ) = 4 × 10-4 m = .4 mm
Hence nearest maximum from O is at adistance y = 0.4 mm
-------------------------------
part (v)
Central maximum occurs when phase difference between two rays emerging from slits S1 and S2 is zero.
we have seen from Part (i) ,Net phase difference at O = Δφ2 - Δφ1 = (80/3)π
Equivalenet path difference = (80/3)π × ( λ / 2π ) = (40/3) λ
To reduce above path difference , required angular position θ is determined from the following expression
d sin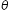
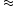 d tan
d tan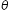 = (40/3) λ
= (40/3) λ
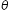
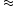 d tan
d tan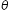 = (40/3) λ
= (40/3) λ d tan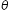 = d ( y / D ) = (40/3) λ
= d ( y / D ) = (40/3) λ
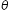 = d ( y / D ) = (40/3) λ
= d ( y / D ) = (40/3) λy = (40/3d) λ = [ 40 / ( 3 × 10-3 ) ] ( 6000 × 10-10 ) = 8 × 10-3 m = 8 mm
Hence central maximum occurs at a point 8 mm above O
-------------------------------------------------------------------
part ( vi )
Path difference at a distance 4 mm above O is determined as
Δp = d sinθ ≈ d tanθ = 10-3 × (4/1000) = 4 × 10-6 m
Equivalent phase difference = 4 × 10-6 × ( 2π / λ ) = 4 × 10-6 × [ 2π / ( 6000 × 10-10 ) ]
Equivalent phase difference =(40/3)π
Phase didfference at a distance 4 mm above O = (80/3)π - (40/3)π = (40/3)π
IR = I1 + I2 + 2 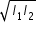 cosΔφ
cosΔφ
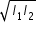 cosΔφ
cosΔφ (Io/2) + 2Io + 2 [ (Io/2)(2Io) ]1/2 cos [ (40/3)π ) = (3/2) Io
If we denote maximum intensity (9/2) Io = I ,
then Intensity at 4 mm above O = { [ (3/2) Io ] / [ (9/2) Io ] } × I = (1/3) I
-----------------------------------------------------------------------------------------------
Answered by Thiyagarajan K | 17 Jul, 2022, 11:49: PM
JEE main - Physics
Asked by beemravumarsukola | 16 Oct, 2023, 07:02: AM
JEE main - Physics
Asked by vinuthaks966 | 27 Sep, 2023, 06:07: AM
JEE main - Physics
Asked by 3047-manvir | 04 Jul, 2022, 12:30: PM
JEE main - Physics
Asked by gokulmohan4002 | 15 May, 2022, 06:23: PM
JEE main - Physics
Asked by kallakurisujatha63 | 24 Feb, 2021, 03:02: PM
JEE main - Physics
Asked by ashutosharnold1998 | 25 Aug, 2019, 01:42: AM
JEE main - Physics
Asked by sameenauzair986 | 28 Jul, 2019, 05:45: PM




