Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 11-science Answered

Without using the Pythagoras theorem, prove that the points (– 2, 2), (8, – 2) and (– 4, – 3) are the vertices of a right angled triangle.
Asked by Topperlearning User | 20 Oct, 2016, 03:05: AM
answered-by-expert Expert Answer

Let these points A (-2, 2), B (8, -2) and C (-4, -3).

 
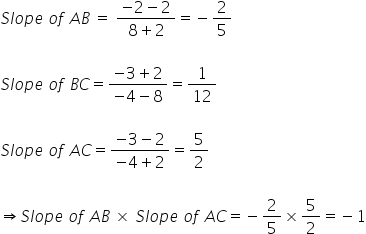
S l o p e space o f space A B space equals space fraction numerator minus 2 minus 2 over denominator 8 plus 2 end fraction equals minus 2 over 5 S l o p e space o f space B C equals fraction numerator minus 3 plus 2 over denominator minus 4 minus 8 end fraction equals 1 over 12 S l o p e space o f space A C equals fraction numerator minus 3 minus 2 over denominator minus 4 plus 2 end fraction equals 5 over 2 rightwards double arrow S l o p e space o f space A B space cross times space S l o p e space o f space A C equals minus 2 over 5 cross times 5 over 2 equals minus 1
 
Therefore, A,B and C are the vertices of a right angled triangle.
Answered by | 20 Oct, 2016, 05:05: AM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 11-science - Maths
Three points P(h,k), Q (x,y) and R (x,y) lie on a line show that (h-x) (y-y)= (k-y) (x-x),
Asked by hrai7387 | 16 Jan, 2023, 07:36: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
determine graphically the vertices of the traingle 3x+3y=10
Asked by bhunias174 | 30 Mar, 2022, 09:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
find a and b so that the lines ax+8y+b=0,2x+ay-1=0 may be parallel or perpendicular  
Asked by ankitakhokhar56 | 06 Dec, 2019, 02:51: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
If space p space i s space t h e space l e n g t h space o f space p e r p e n d i c u l a r space d r a w n space f r o m space o r i g i n space t o space l i n e space x over a plus y over b space equals space 1 space a n d space a squared comma p squared comma b squared space a r e space i n space A. P. space comma space t h e n space p r o v e space t h a t space a to the power of 4 plus b to the power of 4 space equals space 0 space.
Asked by manish.kkd4 | 20 Feb, 2019, 12:20: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the coordinates of point C, which divides the line segment joining the points D (-2, 5) and E (4, 6) in the ratio 2 : 3.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
If the slope of line joining the points (2, 3) and (4, -5) is equal to the slope of line joining the points (x, 5) and (5, 6). Find the value of x.
Asked by Topperlearning User | 26 Sep, 2014, 09:43: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the slope of line which passes through the point (5, 6) and the mid-point of line joining the points (4, 6) and (-3, 7).
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find the point which divides the line segment joining the points A (5, 7) and B (8, 4) in the ratio 3 : 5.
Asked by Topperlearning User | 26 Sep, 2014, 01:57: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
If three points (3, 6), (-5, 7) and (x, 1) are collinear, find the value of x.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 11-science - Maths
Find a point on the Y-axis, which is equidistant from the points (-3, 4) and (5, 6).
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×