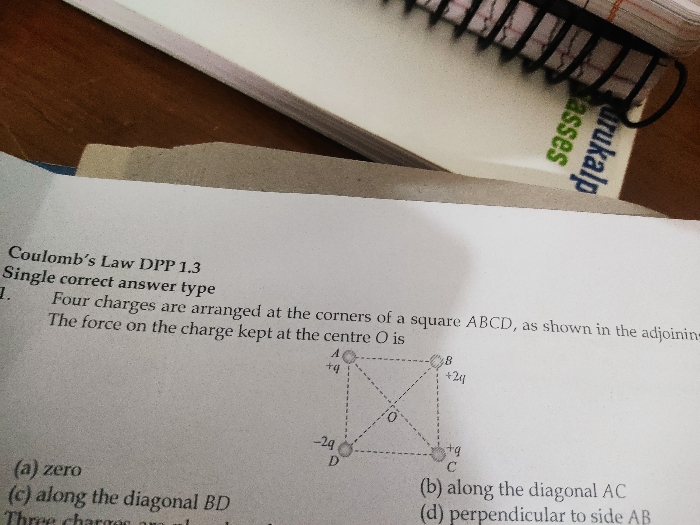Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

JEE Class main Answered

What is the centre of mass of pyramid? Explain briefly with examples
Asked by polyrelation | 21 Oct, 2019, 10:11: PM
answered-by-expert Expert Answer
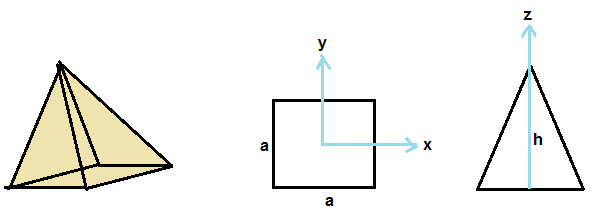
A regular pyramid has square base and triangular faces as lateral sides. 
Let us have x-y-z coordinate system with origin coincide with centre of square base.
let x-y plane is parallel to square base and z-axis coincides with vertical axis of pyramid.
 
centre of mass of 3-dimensional solid is given as
 
begin mathsize 14px style z subscript c m space end subscript equals space fraction numerator integral subscript z m i n end subscript superscript z m a x end superscript integral subscript y m i n end subscript superscript y m a x end superscript integral subscript x m i n end subscript superscript x m a x end superscript z d x d y d z over denominator integral subscript z m i n end subscript superscript z m a x end superscript integral subscript y m i n end subscript superscript y m a x end superscript integral subscript x m i n end subscript superscript x m a x end superscript d x d y d z end fraction end style
where zmin and zmax are lower and upper limits of integration. For our pyramid, zmin = 0, zmax = h.
 
ymax and ymin are y-limits.   xmax and xmin are x-limits.
 
x and y limits are obtained from the sides of square cross section at a given height as shown below
 
 
 
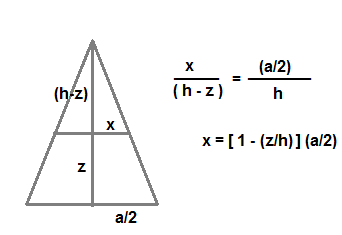
centre of mass of pyramid is obtained  as begin mathsize 14px style z subscript c m space end subscript equals space fraction numerator integral subscript 0 superscript h integral subscript negative left square bracket 1 minus left parenthesis z divided by h right parenthesis right square bracket left parenthesis a divided by 2 right parenthesis end subscript superscript left square bracket 1 minus left parenthesis z divided by h right parenthesis right square bracket left parenthesis a divided by 2 right parenthesis end superscript integral subscript negative left square bracket 1 minus left parenthesis z divided by h right parenthesis right square bracket left parenthesis a divided by 2 right parenthesis end subscript superscript left square bracket 1 minus left parenthesis z divided by h right parenthesis right square bracket left parenthesis a divided by 2 right parenthesis end superscript z d x d y d z over denominator integral subscript 0 superscript h integral subscript negative left square bracket 1 minus left parenthesis z divided by h right parenthesis right square bracket left parenthesis a divided by 2 right parenthesis end subscript superscript left square bracket 1 minus left parenthesis z divided by h right parenthesis right square bracket left parenthesis a divided by 2 right parenthesis end superscript integral subscript negative left square bracket 1 minus left parenthesis z divided by h right parenthesis right square bracket left parenthesis a divided by 2 right parenthesis end subscript superscript left square bracket 1 minus left parenthesis z divided by h right parenthesis right square bracket left parenthesis a divided by 2 right parenthesis end superscript d x d y d z end fraction end style
from the above integration, we get zCM = h/4
 
Hence centre of mass of regular pyramid is at axis and at a height h/4 from base, where h is height of pyramid
Answered by Thiyagarajan K | 22 Oct, 2019, 02:31: PM

Application Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Physics
find current
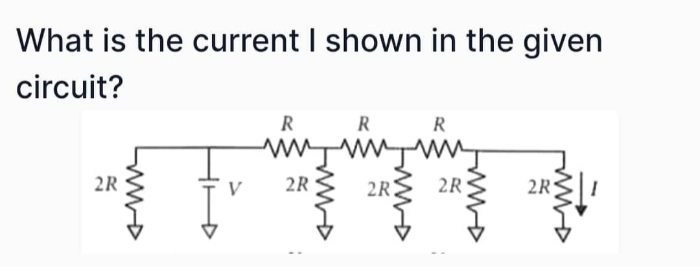
question image
Asked by arivaryakashyap | 23 Apr, 2024, 10:40: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Three equal charges, 2⋅0 × 10 − 6 C each, are held fixed at the three corners of an equilateral triangle of side 5 cm. Find the Coulomb force experienced by one of the charges due to the rest two.
question image
Asked by ratnadeep.dmr003 | 21 Apr, 2024, 11:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Time period for a simple harmonic motion (d ^ 2 * x)/(d * t ^ 2) =- mu xis:
Asked by ksahu8511 | 19 Apr, 2024, 11:55: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
find the acceleration
question image
Asked by mohammedimroz | 13 Apr, 2024, 09:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
solution of 12th question
question image
Asked by medhamahesh007 | 02 Apr, 2024, 11:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
if Bi with a mass number 211 and atomic number 83 undergoes beta decay the resultant daughter nuclei will be
Asked by gundlasumathi93 | 31 Mar, 2024, 02:13: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
four charges are arranged at corners of square abcd as in figur the force on charge kept at centre o is
question image
Asked by chhayasharma9494 | 31 Mar, 2024, 12:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two small conducting spheres each of mass 9×10‐⁴kg qre suspended from the same point by non conducting strings of length 100cm. they are given equal and similar charges until the strings are rqually inclined at 45° each to the vertcal. The charge on each sphere is
Asked by archithateja3 | 30 Mar, 2024, 10:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
how to draw straight line graph and how to identify y-intercept and slope
Asked by Machinenineha | 27 Mar, 2024, 05:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Help me
question image
Asked by nandichandi33 | 24 Mar, 2024, 09:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×