CBSE Class 12-science Answered

(a) Polarization

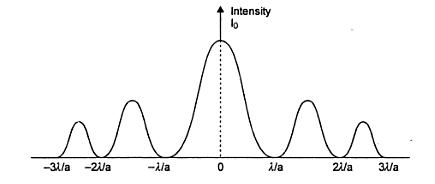
(b) (i) In diffraction all the bright fringes do not have same intensity bright bands are of decreasing intensity. In interference, all bright fringes have same intensity.

(ii) Diffraction is phenomena of bending light around the corners of an obstacle or aperture in the path of height. Interference is the phenomena of redistribution of light energy on account of superposition of light waves from two coherent sources.

(iii) In interference the width of the bands are same. In diffraction the width of the fringes are unequal.

(c)

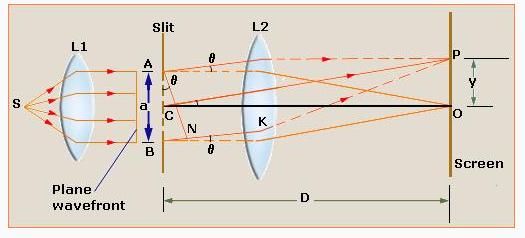
Consider a parallel beam of light from a lens falling on a slit AB. As diffraction occurs, the pattern is focused on the screen XY with the help of lens L₂.

Each point on the unblocked portion of plane wavefront AB sends out secondary wavelets in all directions. The waves from points equidistant from the center C lying on the upper and lower half reach the point O with path difference being zero and hence reinforce each other producing a maximum intensity at the point 0.

Consider a point 'P' on the screen. The intensity at P will depend on the path difference between the secondary waves emitted from the corresponding point of the wavefront. Consider a set of waves making an angle with CO. Draw AN perpendicular to BK. The path difference between the secondary waves reaching P from A and B = BN = AB sin = a sin

where AB = a Is the width of the aperture.

If path difference is , point P will be of minimum intensity. The whole wave front can be considered to be divided into two halves, i.e., CA and CB. If the path difference between the secondary waves from A and B is , then the path difference between secondary waves from A and C will be /2 and the path difference between secondary waves from B and C will be /2. Also for every point in the upper half AC, there is a corresponding point in the lower half CB for which the path difference between the waves is /2. So P is a point of destructive interference.

For nth secondary minimum,

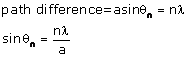
For nth secondary maximum,

where n=1,2,3……., an integer