CBSE Class 12-science Answered

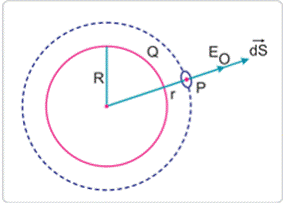
Consider a spherical Gaussian surface of radius r (›R), concentric with given shell. If is electric field outside the shell, then by symmetry, electric field strength has

same magnitude on the Gaussian surface and is directed radially outward. Also the directions of normal at each point is radially outward, so angle between and is zero at each point. Hence, electric flux through Gaussian surface =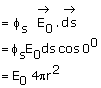

Now, Gaussian surface is outside the given charged shell, so charge enclosed by the Gaussian surface is Q.

Hence, by Gauss's theorem

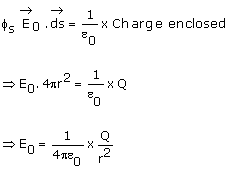
Thus, electric field outside a charged thin spherical shell is same as if the whole charge Q is concentrated at the centre.

Graphically,

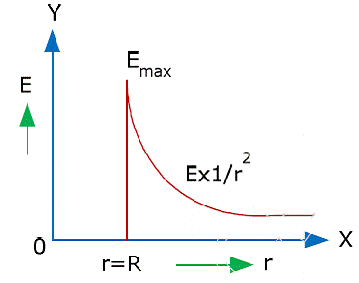
For r ‹ R, there is no strength of electric field inside a charged spherical shell.

For r › R, electric field outside a charged thin spherical shell is same as if the whole charge Q is concentrated at the centre.