CBSE Class 9 Answered
Two circles of radii 10 cm and 8 cm intersect
each other at two points, and the length of the common chord is 12 cm. Find
the distance between their centers.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
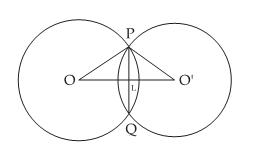
Let O and O' be the centers of the circle of radii 10 cm and 8 cm respectively.
Let PQ be their common chord.
We have,
OP = 10 cm
O'P = 8 cm
PQ = 12 cm
![]() (Perpendicular
from the center of the circle to a chord bisects the chord).
(Perpendicular
from the center of the circle to a chord bisects the chord).
In
right ![]() OLP, we have
OLP, we have
OP2 = OL2 + PL2
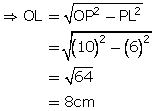
In
right ![]() O'LP we have
O'LP we have
(O'P)2 = (PL)2 + (O'L)2
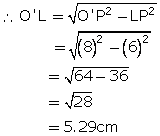
![]() OO' = 8 + 5.29
OO' = 8 + 5.29
= 13.29 cm
Answered by | 04 Jun, 2014, 03:23: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by subbusuchi1978 | 05 Nov, 2023, 10:24: AM
CBSE 9 - Maths
Asked by rameshsonkar1234ramesh | 21 Dec, 2022, 11:03: PM
CBSE 9 - Maths
Asked by chalkekalyani80 | 06 Mar, 2022, 11:25: AM
CBSE 9 - Maths
Asked by tejvinder3r | 27 Jan, 2020, 10:27: AM
CBSE 9 - Maths
Asked by arvindhsb2005 | 14 Jan, 2020, 09:14: PM
CBSE 9 - Maths
Asked by sambitgenius2005 | 24 Apr, 2019, 08:03: PM
CBSE 9 - Maths
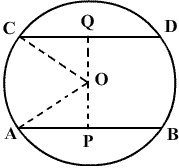
Asked by Topperlearning User | 18 Aug, 2017, 09:07: AM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 14 Feb, 2014, 02:05: PM