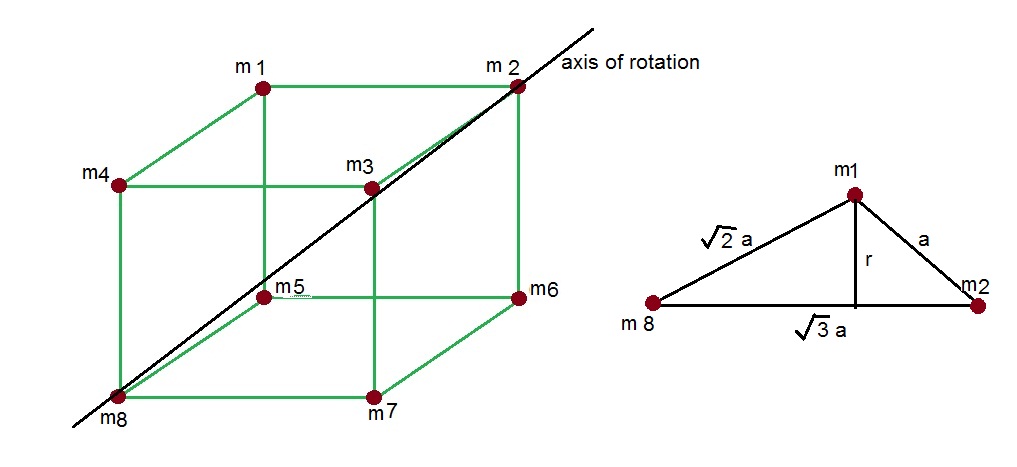
there is a cubic frame,on each corner a pont mass'm' are kept,tell about momet of inertia if axis is pass through body diagonal of cube.each side of cube is 'a'.
Asked by Kunal
5th December 2017,
4:49 PM
Answered by Expert
Answer:
Let m1, m2,.....m8 are the point masses placed at each corner of the cube. let r be the perpendicular distance from m1 to axis of rotation.
the distance r can be calculated from the triangle area shown in figure and the required equations are given below
as per my calculation I am getting r = (0.816)a
m2 and m8 are placed in the axis itself, hence do not contribute for moment of Inertia.
for all other 6 masses the perpendicular distance can be calculated as explained above and all the perpendicular distances are identical.
hence required Moment of Inertia = 6 × m × (0.816)2 × a2 = 3.995 ma2
Answered by Expert
6th December 2017,
3:29 PM
Rate this answer
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
You have rated this answer /10
Your answer has been posted successfully!
RELATED STUDY RESOURCES :
Browse free questions and answers by Chapters
Trending Tags
Latest Questions
JEE Main Mathematics
Asked by amaladelsingh
28th October 2020,
10:24 PM
CBSE X Biology
Asked by reenacharan2008
28th October 2020,
9:11 PM
