CBSE Class 10 Answered
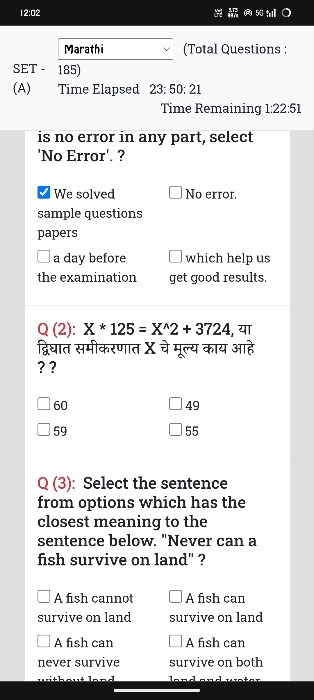
The ratio of the sums of m and n terms of an A.P. is m^2(m square):n^2(n square). S.T. the ratio of the mth and nth terms is (2m-1):2n-1).
Asked by | 26 Jan, 2014, 07:19: AM
The sum of m terms of an A.P is am + m(m-1)d/2.
That is we have, Sum of m terms = am + m^2(d/2) - (md/2)
The sum of n terms of an A.P is an + n(n-1)d/2.
That is we have, Sum of n terms = an + n^2(d/2) - (nd/2)
Given that, Sum of m terms:Sum of n terms =
= [am + m^2(d/2) - (md/2)] : [an + n^2(d/2) - (nd/2)] = m^2:n^2
That is we have,
[2a+(m-1)d]:[2a+(m-1)d] = m:n
That is,
2a(n-m)=d[(n-1)m-(m-1)n]
That is,
2a(n-m)=d(n-m)
That is,
d = 2a
Now, mth term:nth term=[a+(m-1)d]:[a+(n-1)d]
That is,
mth term:nth term=[a+(m-1)2a]:[a+(n-1)2a]
That is,
mth term:nth term=(2m-1):(2n-1)
Answered by | 29 Jan, 2014, 04:38: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
CBSE 10 - Maths
Asked by rrajansinghakb199 | 08 Apr, 2024, 05:12: PM
CBSE 10 - Maths
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
CBSE 10 - Maths
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
CBSE 10 - Maths
Asked by muttenenimalleswarrao | 29 Mar, 2024, 08:32: PM
CBSE 10 - Maths
Asked by pathakvaishnavi9139 | 23 Mar, 2024, 10:45: AM
CBSE 10 - Maths
Asked by mustafahssn786 | 23 Mar, 2024, 06:25: AM
CBSE 10 - Maths
Asked by choudharyniki001 | 22 Mar, 2024, 08:49: AM
CBSE 10 - Maths
Asked by jagdishdabang79 | 18 Mar, 2024, 08:40: PM