Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

The following table shows the number of runs scored by a certain batsman in different overs: Over 50-55 55-60 60-65 65-70 70-75 75-80 No. of runs 2 8 12 24 38 16 Change the distribution to a "more than" type distribution, and draw its OGIVE on the graph.
Asked by Topperlearning User | 27 Jul, 2017, 04:20: PM
answered-by-expert Expert Answer

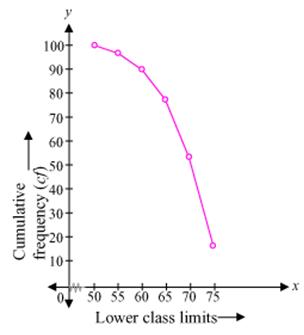
We can obtain cumulative frequency distribution of more than type as following - 

Over

(lower class limits)

Cumulative frequency

More than or equal to 50

100

More than or equal to 55

100 - 2 = 98

More than or equal to 60

98 - 8 = 90

More than or equal to 65

90 - 12 = 78

More than or equal to 70

78 - 24 = 54

More than or equal to 75

54 - 38 = 16

Now taking lower class limits on x-axis and their respective cumulative frequencies on y-axis we can obtain its ogive as follows.

 

Answered by | 27 Jul, 2017, 06:20: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
I want rs agaarwal class 10 chapter statics solution
Asked by shoaibkhan87277 | 17 Oct, 2020, 02:58: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Please solve.
question image
Asked by karanbora625 | 05 May, 2020, 11:03: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
WHEN LESS THAN OR EQUAL TO IS GIVEN..HOW TO DRAW AN OGIVE
Asked by mad | 06 Mar, 2019, 03:45: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Construct a cumulative frequency distribution table of the following distribution: C.I. 12.5-17.5 17.5-22.5 22.5-27.5 27.5-32.5 32.5-37.5  F 2 22 19 14 13   C.I. 12.5-17.5 17.5-22.5 22.5-27.5 27.5-32.5 32.5-37.5  F 2 22 19 14 13
Asked by Topperlearning User | 13 Feb, 2014, 04:58: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Draw a 'more than ogive' for the given data. Marks (more than) No. of students 10 50 20 41 30 39 40 22 50 11 60 6
Asked by Topperlearning User | 25 Feb, 2014, 04:38: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Draw a 'more than ogive' for the given data. Marks (more than) No. of students 0 50 10 42 20 38 30 23 40 12 50 5
Asked by Topperlearning User | 25 Feb, 2014, 04:39: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Draw a 'less than ogive' for the given data. Marks 10-20 20-30 30-40 40-50 50-60 No. of students 2 4 7 6 1
Asked by Topperlearning User | 25 Feb, 2014, 04:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The annual rainfall record of a city for 66 days is given in the following table. Construct a less than and more than ogive and hence find the median. Rainfall (in cm) 0-10 10-20 20-30 30-40 40-50 50-60 No. of days 22 10 8 15 5 6
Asked by Topperlearning User | 13 Feb, 2014, 05:05: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The following distribution gives the daily income of 50 workers of a factory. Daily income (in Rs) 10-12 12-14 14-16 16-18 18-20 No. of workers 11 4 2 3 5 Convert the above distribution to a less than type cumulative frequency distribution.
Asked by Topperlearning User | 03 Nov, 2017, 10:10: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Convert the given frequency distribution to a more than type cumulative frequency distribution. Marks 0-10 10-20 20-30 30-40 40-50 50-60 60-70 70-80 80-90 No. of students 2 2 3 4 6 6 5 2 4
Asked by Topperlearning User | 25 Feb, 2014, 04:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×