Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

ICSE Class 10 Answered

tan a + sin a = m & tan a - sin a = n prove that m2 - n2 4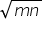square root of m n end root
Asked by Vinay | 06 Apr, 2017, 01:47: PM
answered-by-expert Expert Answer

Given that tan a + sin a = m and tan a - sin a = n 

Consider,

mn = (tan a + sin a) (tan a - sin a) 

mn = tan2 a - sin2 a =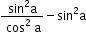begin mathsize 12px style fraction numerator sin squared straight a over denominator space cos squared space straight a end fraction minus sin squared straight a end style

mn = begin mathsize 12px style sin squared space straight a open parentheses fraction numerator 1 over denominator space cos squared space straight a end fraction minus 1 close parentheses end style

mn = begin mathsize 12px style sin squared space straight a open parentheses fraction numerator 1 minus space cos squared space straight a over denominator space cos squared space straight a end fraction close parentheses end style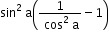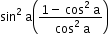  

mn = tan2 a  × sin2 a      .......( i ) 

Consider,

LHS = m2 - n2

        = (tan a + sin a )2 - (tan a - sin a)2 

        = tan2 a  + sin2 a   + 2 tan A sin A - tan2 a   - sin2 a  + 2 tan A sin A 

        = 4 tan A sin A 

        = 4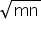square root of mn [from equation ( i )] 
        = RHS

Hence proved.

If you have any other query, do attend the FREE webinar (Online Class) on 12th April from 4 pm to 5 pm.

Answered by | 06 Apr, 2017, 02:11: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
ICSE 10 - Maths
cot A - 1/ 2 - sec² = cot A / 1 + tan A
Asked by bhagvantingre | 24 Apr, 2024, 03:05: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
solve xdy-ydx=0
Asked by shaikafridi860 | 21 Apr, 2024, 11:22: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
if a is an acute angle and sec a = 17/8, find all other trigonometric rarios of angle a ( using trigonometric indentities).
Asked by aritramalakar4 | 13 Apr, 2024, 08:33: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
3√2x×x-5x-√2
question image
Asked by ashwanikaler9 | 11 Apr, 2024, 01:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
prove that
question image
Asked by botlarajshekhar | 22 Mar, 2024, 09:37: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
Mr. Gupta invested Rs. 33000 in buying Rs.100 shares of a company at 10% premium. The dividend declared by the company is 12% . Find: (a) the number of shares purchased by him. (b) his annual dividend
Asked by sagarmishra | 15 Mar, 2024, 03:22: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
 (a+b)²
Asked by dadoosumeksha | 13 Mar, 2024, 09:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
sheethal has a recurring deposit account in a bank and deposit rupees 300 and at rate of interest of 7℅ and recieved rupees 7725 on maturity, find the time which would the account will be held
Asked by jesnamariaroy2626 | 10 Mar, 2024, 11:28: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
if abc are in Continued proportion then prove that 3a2-4ab+5b2/3b2-4bc+5c2=a/c
Asked by vrj.parmar369 | 07 Mar, 2024, 11:27: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
ICSE 10 - Maths
sole
question image
Asked by ronaldlhouvum | 22 Feb, 2024, 02:42: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×