Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

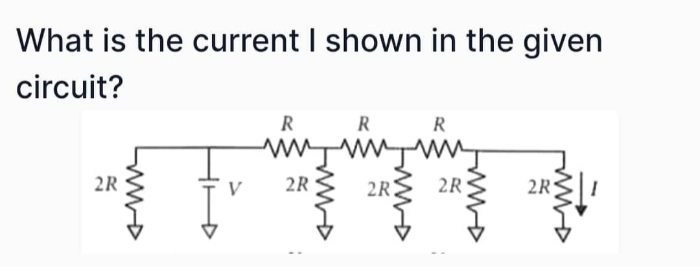
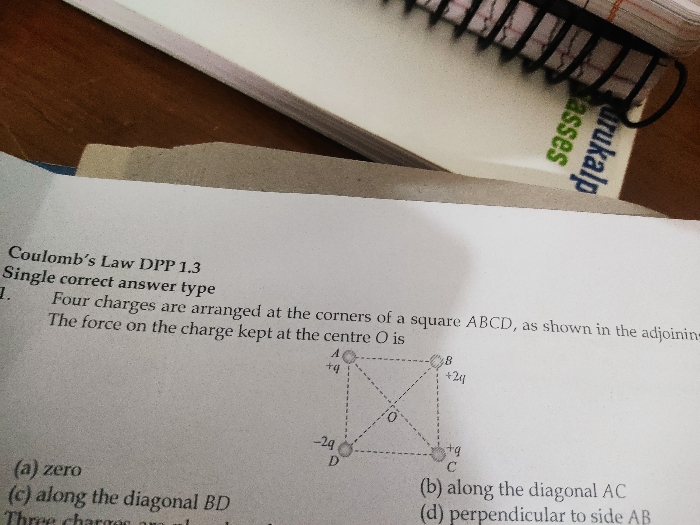JEE Class main Answered

solve
question image
Asked by adjacentcalliber10 | 18 May, 2019, 01:17: PM
answered-by-expert Expert Answer
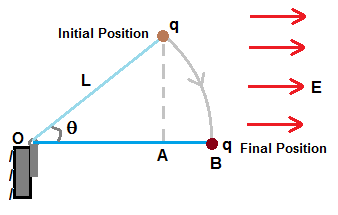
Figure shows the particle of mass m and charge q  at one end of rod of length L . 
Other end of rod is hinged at O so that the rod rotates freely in the plane of figure.
 
Direction of electric field E is as shown in figure.

From the position as shown by angle θ that is made by the rod with field direction  to
the position OAB as shown in figure  which is parallel to field, the particle is displaced to a
distance AB in the direction of electric field.  Workdone W by the particle for this displacement is given by
 
W = qE×AB = q E L (1 - cosθ)  .........................(1)  
 
This workdone will be equal to the kinetic energy of particle when the rod  is  parallelel to field.
 
Hence we have, (1/2) m v2 = q E L (1 - cosθ)  ........................(2)
 
where m is mass of particle and v is speed of particle when it reahes the position B.
 
hence speed of particle v is given by,  v = [ 2q E L (1 - cosθ) / m ]1/2
Answered by Thiyagarajan K | 19 May, 2019, 11:55: AM

Application Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
JEE main - Physics
find current
question image
Asked by arivaryakashyap | 23 Apr, 2024, 10:40: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Three equal charges, 2⋅0 × 10 − 6 C each, are held fixed at the three corners of an equilateral triangle of side 5 cm. Find the Coulomb force experienced by one of the charges due to the rest two.
question image
Asked by ratnadeep.dmr003 | 21 Apr, 2024, 11:06: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Time period for a simple harmonic motion (d ^ 2 * x)/(d * t ^ 2) =- mu xis:
Asked by ksahu8511 | 19 Apr, 2024, 11:55: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
find the acceleration
question image
Asked by mohammedimroz | 13 Apr, 2024, 09:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
solution of 12th question
question image
Asked by medhamahesh007 | 02 Apr, 2024, 11:11: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
if Bi with a mass number 211 and atomic number 83 undergoes beta decay the resultant daughter nuclei will be
Asked by gundlasumathi93 | 31 Mar, 2024, 02:13: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
four charges are arranged at corners of square abcd as in figur the force on charge kept at centre o is
question image
Asked by chhayasharma9494 | 31 Mar, 2024, 12:47: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
two small conducting spheres each of mass 9×10‐⁴kg qre suspended from the same point by non conducting strings of length 100cm. they are given equal and similar charges until the strings are rqually inclined at 45° each to the vertcal. The charge on each sphere is
Asked by archithateja3 | 30 Mar, 2024, 10:23: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
how to draw straight line graph and how to identify y-intercept and slope
Asked by Machinenineha | 27 Mar, 2024, 05:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
JEE main - Physics
Help me
question image
Asked by nandichandi33 | 24 Mar, 2024, 09:21: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×