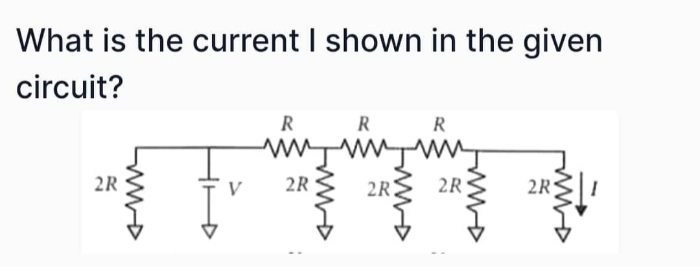
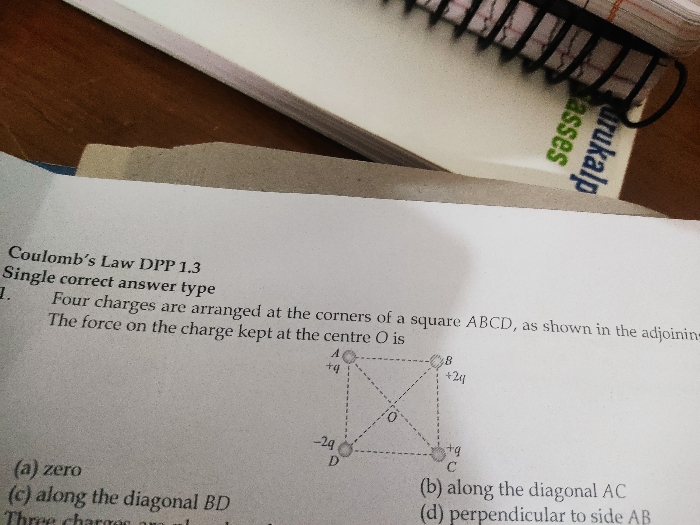JEE Class main Answered
solve all the two paragraph question
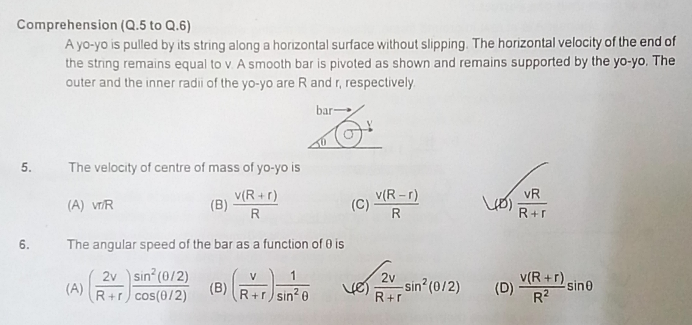
Asked by sarveshvibrantacademy | 18 May, 2019, 11:52: AM
Expert Answer
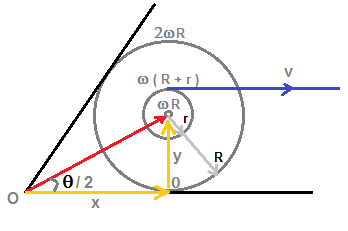
when yo-yo rolls with angular velocity ω without slipping, velocity is zero at the point of contact at bottom and
velocity is 2ωR at top most point as marked in figure. Where R is major radius of yo-yo.
Hence velocity of centre of mass = ωR ..................(1)
if we linearly interpolate, at a point where the yo-yo is pulled by unwinding the string attached, velocity is ω(R+r).
But at this point yo-yo is pulled with speed v, hence v = ω(R+r) ....................(2)
if we substitute for ω in eqn.(1), using eqn.(2), then we have, velocity of centre of mass = v R/(R+r) .............................(3)
If θ is the angle subtended by bar with horizontal surface, then we have (refer figure), tan(θ/2) = y/x = R/x .......................(4)
if we differentiate equation (4), sec2(θ/2) (1/2) (dθ/dt) = -R/x2 (dx/dt) .....................(5)
By substituting x using eqn.(4) and substituting (dx/dt) as velocity of centre of mass from eqn.(3),
we rewrite eqn.(5) as sec2(θ/2) (1/2) (dθ/dt) = - tan2(θ/2) (1/R) [ v R/(R+r) ]
Hence after simplification of above equation, we get angular velocity of bar, (dθ/dt) = -2 sin2(θ/2) [ v / (R+r) ]
(-ve sign of angular velocity indicates, direction of rotation is clockwise )
Answered by Thiyagarajan K | 19 May, 2019, 03:39: PM
Application Videos
-
Elastic potential energy_Restoring force and spring con ...
In this video, the restoring force and spring constant is explained. The vi... -
Expression of Elastic potential energy_2
This video describes the potential energy of spring when it is compressed o... -
Potential Energy Curve
This video describes the potential energy curve and ature of forces based o... -
Work done by static friction
This video describes effect of static friction on the work done by the obje... -
Work done in conservative field - 1
The concept of conservative field, types of conservative forces and example...
JEE main - Physics
Asked by arivaryakashyap | 23 Apr, 2024, 10:40: AM
ANSWERED BY EXPERTJEE main - Physics
Asked by ratnadeep.dmr003 | 21 Apr, 2024, 11:06: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by ksahu8511 | 19 Apr, 2024, 11:55: AM
ANSWERED BY EXPERTJEE main - Physics
Asked by mohammedimroz | 13 Apr, 2024, 09:48: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by medhamahesh007 | 02 Apr, 2024, 11:11: AM
ANSWERED BY EXPERTJEE main - Physics
Asked by gundlasumathi93 | 31 Mar, 2024, 02:13: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by chhayasharma9494 | 31 Mar, 2024, 12:47: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by archithateja3 | 30 Mar, 2024, 10:23: PM
ANSWERED BY EXPERTJEE main - Physics
Asked by Machinenineha | 27 Mar, 2024, 05:28: PM
ANSWERED BY EXPERT
