Sir pls solve this question.
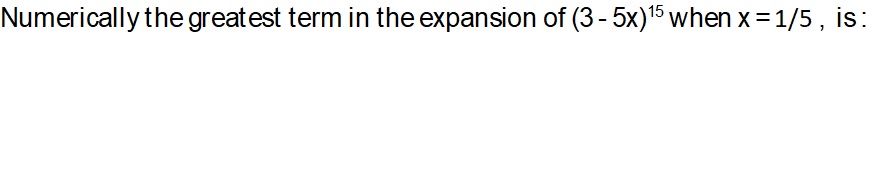

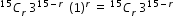
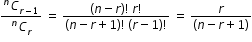
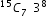
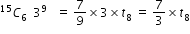
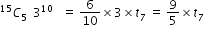
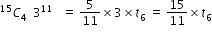
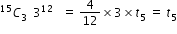
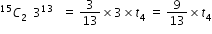
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
You have rated this answer /10
Browse free questions and answers by Chapters
- 1 Sequences and Series
- 2 Mathematical Reasoning
- 3 Differential Equations
- 4 Three Dimensional Geometry
- 5 Complex Numbers and Quadratic Equations
- 6 Permutations and Combinations
- 7 Matrices and Determinants
- 8 Vector Algebra
- 9 Trigonometry
- 10 Integral Calculus
- 11 Sets, Relations and Functions
- 12 Limit, Continuity and Differentiability
- 13 Statistics and Probability
- 14 Co-ordinate Geometry
- 15 Mathematical Induction
- 16 Binomial Theorem and its Simple Applications
