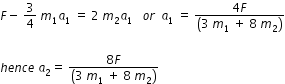Plank is pushed by the force F from left to right. This force makes the plank to move from left to right.
Hence at point of contact, friction force f will act towards left in the plank as shown in figure.
At plank we have, ( F - f ) = m2×a2 ......................(1)
where a2 is acceleration of the plank.
At point of contact between plank and cylinder, as per newton's thrid law, there is a reaction force f acting on the cylinder.
This reaction force is towards right as shown in figure. ( This reaction force is opposite to friction force acting on the plank. )
This reaction force f is trying to move the point of contact by an acceleration aCM = f / m1 towards right.
Also this reaction force f is trying to rotate the cylinder of radius R about its centre of mass in clockwise direction.
hence we have, 
from eqn.(2) we have, 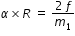
acceleration at point of contact P, 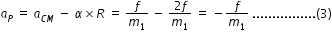
as per eqn.(3), point of contact P move towards left. Hence friction force f ' acts towards right as shown in figure.
Let a1 be the acceleration of Centre of mass of cylinder.
If there is no slipping between plank and cylinder, we have 
By applying Newton's law to cylinder, we can write, 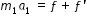 ......................(5)
......................(5)
Also these forces trying to rotate the cylinder and due to rotational motion, we can write,
we can solve eqns.(5) and (6) to get f and f ' ;  ....................(7)
....................(7)
using eqn.(1), (4) and (7), we write
magnitudes of friction forces f and f ' can be calculated using eqn.(7) by substituting the value of a1



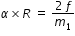
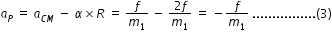

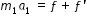 ......................(5)
......................(5)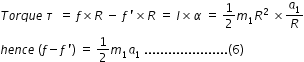
 ....................(7)
....................(7)