JEE Class main Answered

Show the following matrix is diagonalizable

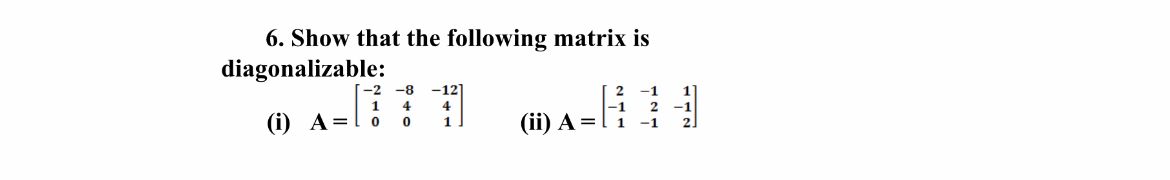
Asked by aryansohanyadav205 | 26 Nov, 2022, 09:20: PM

Expert Answer

(i) To prove A is diagonalizable where A = [-2 -8 -12 // 1 4 4 // 0 0 1]

Consider, A - lambda I = 0

open vertical bar straight A minus λI close vertical bar equals open vertical bar open square brackets table row cell negative 2 end cell cell negative 8 end cell cell negative 12 end cell row 1 4 4 row 0 0 1 end table close square brackets minus open square brackets table row straight lambda 0 0 row 0 straight lambda 0 row 0 0 straight lambda end table close square brackets close vertical bar equals open vertical bar table row cell negative 2 minus straight lambda end cell cell negative 8 end cell cell negative 12 end cell row 1 cell 4 minus straight lambda end cell 4 row 0 0 cell 1 minus straight lambda end cell end table close vertical bar equals left parenthesis negative 2 minus straight lambda right parenthesis left parenthesis 4 minus straight lambda right parenthesis left parenthesis 1 minus straight lambda right parenthesis plus 8 left parenthesis 1 minus straight lambda right parenthesis equals left parenthesis negative 8 minus 4 straight lambda plus 2 straight lambda plus straight lambda squared plus 8 right parenthesis left parenthesis 1 minus straight lambda right parenthesis equals left parenthesis straight lambda squared minus 2 straight lambda right parenthesis left parenthesis 1 minus straight lambda right parenthesis equals straight lambda left parenthesis straight lambda minus 2 right parenthesis left parenthesis 1 minus straight lambda right parenthesis open vertical bar straight A minus λI close vertical bar equals 0 space rightwards double arrow straight lambda equals 0 comma space 1 comma space 2 Take space different space values space of space straight lambda space in space left square bracket straight A minus λI right square bracket open square brackets table row cell straight x subscript 1 end cell row cell straight x subscript 2 end cell row cell straight x subscript 3 end cell end table close square brackets equals open square brackets table row 0 row 0 row 0 end table close square brackets Find space values space of space eigen space vectors space straight x subscript 1 comma space straight x subscript 2 comma space straight x subscript 3 Form space straight a space matrix space straight P space with space eigen space vectors space straight x subscript 1 comma space straight x subscript 2 comma space straight x subscript 3 space where space straight x subscript 1 comma space straight x subscript 2 comma space straight x subscript 3 space represents space the space three space different space columns. If space straight P to the power of negative 1 end exponent AP equals straight D space left parenthesis diagonal space matrix right parenthesis space then space straight A thin space is space diagonalizable.

Answered by Renu Varma | 19 Dec, 2022, 09:55: AM

Please Login or Sign up to continue!

JEE Class main Answered

Choose Filters

Open In Ask A Doubt App ?

Get in Touch

Call / Whats App