CBSE Class 10 Answered
show that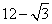 
is irrational.
is irrational.
Asked by Topperlearning User | 25 Jul, 2017, 04:54: PM
Expert Answer
Let 
=
a rational number
rearranging this equation 
Since 12 and are rational number which mean 
is also a rational number. But this contradicts the fact that is an irrational because we already learnt that square roots of prime numbers are irrational. So, we conclude that is irrational.
Answered by | 25 Jul, 2017, 06:54: PM
Application Videos
-
Irrational Numbers
The video explains how to prove that a number is irrational.
-
Rational and Irrational Numbers
The video explains an example based on the concept of Rational and Irrat...
Concept Videos
-
Rational and Irrational Numbers
Discuss rational and irrational numbers and express them on the number lin... -
Rational and Irrational Numbers
Discuss rational and irrational numbers and express them on the number lin... -
Rational and Irrational Numbers
Discuss rational and irrational numbers and express them on the number lin...
CBSE 10 - Maths
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by reddyjaswamth | 10 Jan, 2024, 01:49: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by pv925403 | 07 Jan, 2024, 07:32: PM
ANSWERED BY EXPERT
CBSE 10 - Maths
Asked by abdulqadirmohd028 | 22 Dec, 2023, 12:56: AM
ANSWERED BY EXPERT
CBSE 10 - Maths
Asked by appanaboinakhasim8 | 05 Dec, 2023, 07:01: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by kanchandevi5268 | 03 Nov, 2023, 06:35: AM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by appusingh0840 | 29 Oct, 2023, 01:14: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by jilsmendapara123 | 28 Jul, 2023, 02:44: PM
ANSWERED BY EXPERT
