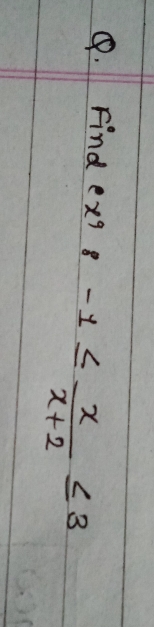
JEE Class main Answered
Q) Prove that the tangent to the circle x^2+y^2=5 at the point (1,-2) also touches the circle x^2+y^2-8x+6y+20=0 and find its point of contact.
Asked by Anish | 08 Mar, 2019, 08:55: PM
Expert Answer
Tangent to circle x2 + y2 = 5 at a point (x1 , y1 ) on circle is xx1 + yy1 = 5
we need a tangent at a point(1, -2) on circle. hence tangent is x - 2y = 5 ............................(1)
If eqn.(1) is also tangent to circle x2 +y2 -8x +6y +20 = 0, then we substitute y = (x-5)/2 in the circle eqn. and
get the point of contact of this tangent
x2 +[ (x-5)2 /4 ] -8x +6 [ (x-5)/2 ] + 20 = 0
after simplification of the above eqn., we get, x2 -6x +9 = 0 or (x-3) = 0 or x = 3
By substituting x =3 in eqn.(1), we get y = -1
Hence point of contact of the tangent given by eqn.(1) to the circle x2 +y2 -8x +6y +20 = 0, is (3, -1)
Verification of eqn.(1) is tangent to circle x2 +y2 -8x +6y +20 = 0 is done by substituting coordinates of point of contact
in tangent equation xx1 + yy1-4(x+x1) +3(y+y1) +20 = 0
x(3) + y(-1) -4(x+3) +3(y-1) +20 = -x +2y + 5 = 0 or x-2y = 5 which is same as eqn.(1)
Answered by Thiyagarajan K | 09 Mar, 2019, 12:22: PM
Application Videos
-
Finding ratio of lengths of sides of a triangle when th ...
This explains how to find the angles of a triangle using the relation betwe... -
Distance of a point lying on the square and circle from ...
The question solved in this video uses the standard equation of a circle is... -
Area of triangle formed by tangent & normal to circ ...
The video explains how to find the area of a triangle formed by the tangent... -
Solving the DE using variable separation method
The video explains to find the solution of a differential equation using th... -
Solution of a Linear DE using Integrating factor
Question solved in the video explains to find the solution of linear differ...
Concept Videos
-
Properties of Inverse Trigonometry Part - 1
This video explains the properties of inverse trigonometric applications an... -
Trigonometric identities and problems
Fundamental trigonometric identities and problems based on them. Sign Conve... -
Graphical representation of inverse trigonometric funct ...
Graphical representation of inverse trigonometric functions and principle ... -
Degree measure and Radian measure ...
This video explains the concept of negative & positive angles, conversion o... -
Continuous and Discontinuous function
Understand the meaning of function to be continuous and discontinuous, comb...
JEE main - Maths
Asked by nirmalraulji5 | 18 Apr, 2024, 09:03: PM
ANSWERED BY EXPERT
JEE main - Maths
Asked by veerababukoppisettiveerababu3 | 17 Apr, 2024, 05:49: PM
ANSWERED BY EXPERTJEE main - Maths
Asked by usakoyalshailesh | 15 Apr, 2024, 09:48: AM
ANSWERED BY EXPERT
JEE main - Maths
Asked by sharmalalita847 | 14 Apr, 2024, 09:21: PM
ANSWERED BY EXPERTJEE main - Maths
Asked by sarthakshukla7275 | 14 Apr, 2024, 01:29: PM
ANSWERED BY EXPERTJEE main - Maths
Asked by ashwinskrishna2006 | 14 Apr, 2024, 11:58: AM
ANSWERED BY EXPERT
JEE main - Maths
Asked by satyampatel95694 | 13 Apr, 2024, 05:35: PM
ANSWERED BY EXPERT
