Q

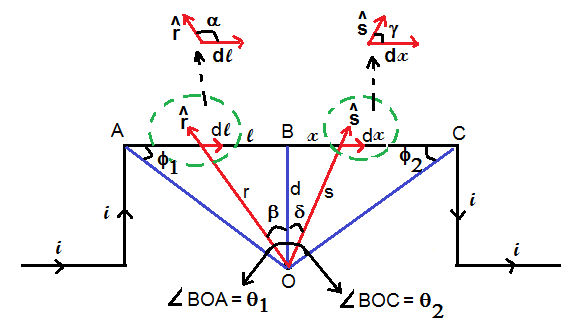
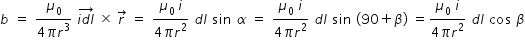
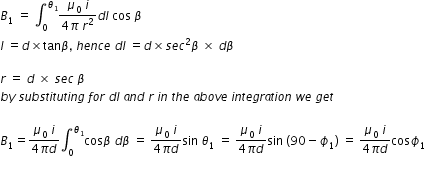
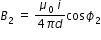
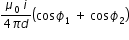
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
You have rated this answer /10
For Franchisee Enquiry
or
You are very important to us
For any content/service related issues please contact on this number
93219 24448 / 99871 78554
Mon to Sat - 10 AM to 7 PM


You have rated this answer /10