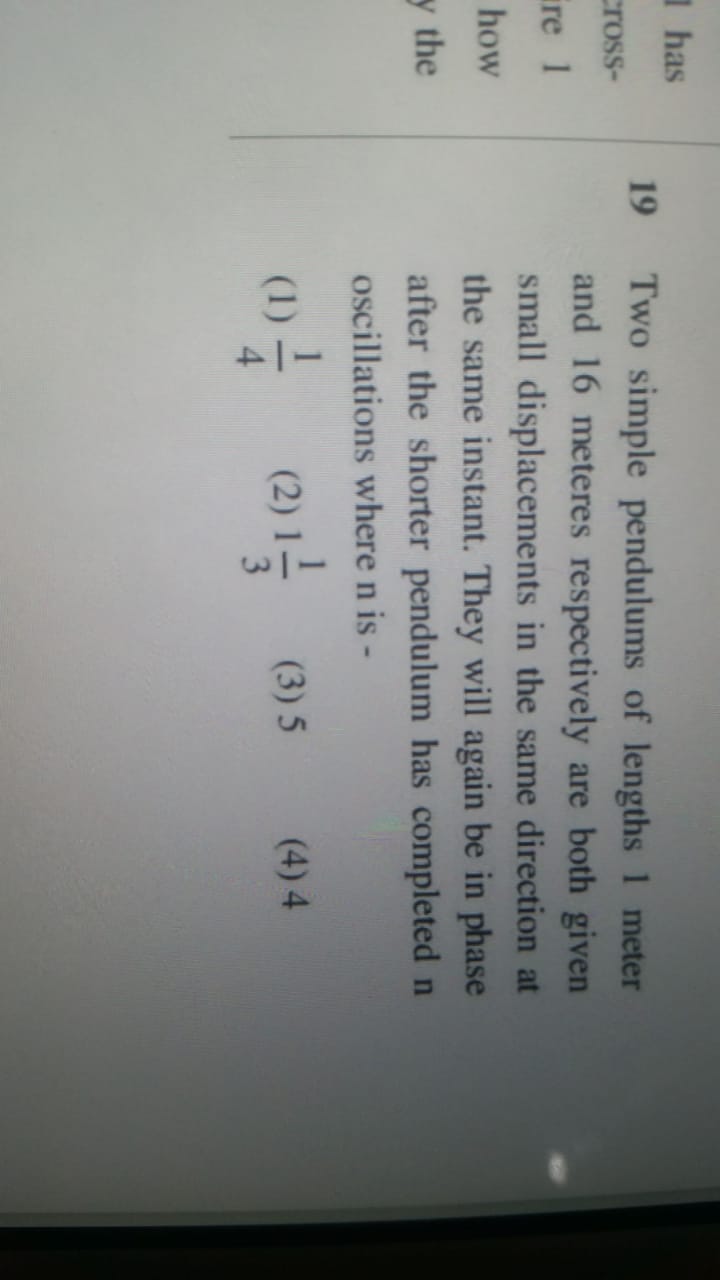CBSE Class 11-science Answered
Prove that the motion of a spring is SHM.
Asked by | 23 Mar, 2013, 01:33: PM
| Consider a mass "m" attached to the end of an elastic spring. The other end of the spring is fixed at the a firm support as shown in figure "a". The whole system is placed on a smooth horizontal surface. If we displace the mass 'm' from its mean position 'O' to point "a" by applying an external force, it is displaced by '+x' to its right, there will be elastic restring force on the mass equal to F in the left side which is applied by the spring. |
|
 |
|
| According to "Hook's Law | |
|
F = - Kx ---- (1)
|
|
| Negative sign indicates that the elastic restoring force is opposite to the displacement. Where K= Spring Constant |
|
| If we release mass 'm' at point 'a', it moves forward to ' O'. At point ' O' it will not stop but moves forward towards point "b" due to inertia and covers the same displacement -x. At point 'b' once again elastic restoring force 'F' acts upon it but now in the right side. In this way it continues its motion from a to b and then b to a. |
|
| According to Newton's 2nd law of motion, force 'F' produces acceleration 'a' in the body which is given by | |
|
F = ma ---- (2)
|
|
| Comparing equation (1) & (2) | |
|
ma = -kx
|
|
|
|
|
| Here k/m is constant term, therefore , | |
|
a = - (Constant)x
or |
|
|
a a -x
|
|
| This relation indicates that the acceleration of body attached to the end elastic spring is directly proportional to its displacement. Therefore its motion is Simple Harmonic Motion. |
Answered by | 25 Mar, 2013, 10:52: AM
Concept Videos
CBSE 11-science - Physics
Asked by sy123946 | 07 Apr, 2024, 04:23: PM
CBSE 11-science - Physics
Asked by goludada1479 | 06 Feb, 2024, 07:35: PM
CBSE 11-science - Physics
Asked by sakshiiiyadav9336 | 02 Feb, 2024, 09:37: AM
CBSE 11-science - Physics
Asked by saikapianharsh7079 | 21 May, 2022, 08:23: PM
CBSE 11-science - Physics
Asked by snehasahu824 | 03 Mar, 2020, 10:06: AM
CBSE 11-science - Physics
Asked by polyrelation | 04 Dec, 2019, 10:35: AM
CBSE 11-science - Physics
Asked by devvratagrahari | 02 Dec, 2019, 06:44: AM
CBSE 11-science - Physics
Asked by SELVA | 06 Jul, 2019, 03:25: PM