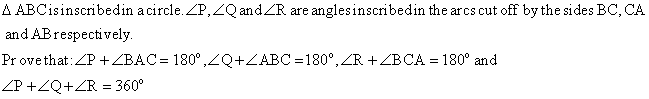CBSE Class 9 Answered
Prove that the circle drawn with any side of a rhombus as a diameter, passes through the point intersection of its diagonals.
Asked by sujaysarkar84 | 07 Mar, 2015, 10:54: AM
Let PQRS be a rhombus with diagonals PR and QS which intersect at O.
We know that diagonals of rhombus intersect each other at right angles. Therefore

Here we have circles passing through PQ, QR, RS, SP as diametre and they pass through O.
For the circle with PQ as diameter, we have angle POQ inscribed in the semi-circle. Also angle inscribed in a semi-circle is a right angle.
Thus, the circle passes through O.
This is true for any circle constructed on any of the side of rhombus.
Therefore, circle with the side of rhombus as diameter passes through the point of intersection of its diagonals.
Answered by Mili Hariyani | 07 Mar, 2015, 01:21: PM
Application Videos
Concept Videos
CBSE 9 - Maths
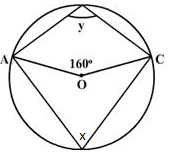
Asked by sdmbotch1123 | 17 Dec, 2022, 09:39: PM
CBSE 9 - Maths
Asked by nirup6957 | 20 Jan, 2020, 07:10: PM
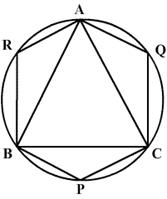
CBSE 9 - Maths
Asked by mukhreetyadav1972 | 29 Dec, 2019, 07:34: PM
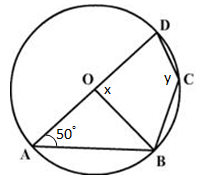
CBSE 9 - Maths
Asked by Topperlearning User | 04 Oct, 2017, 02:06: PM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Oct, 2017, 02:03: PM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Oct, 2017, 01:55: PM












 .
.