CBSE Class 10 Answered
Prove that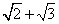 
is an irrational number.
is an irrational number.
Asked by Topperlearning User | 25 Jul, 2017, 04:54: PM
Expert Answer
Suppose 
is not an irrational number, then it must be a rational number.
So let =q where q is a rational number.
)=
=
=
So here we have an equation with its left side is a rational number(as the set of rational numbers is closed under subtraction and division i.e the subtraction and division of two rational numbers is always a rational number)and so its right side must also be a rational number.
is a rational number
Which is a contradiction. So our basic assumption must be wrong.
=q where q is a rational number,is wrong
is an irrational number.
Hence proved.
Answered by | 25 Jul, 2017, 06:54: PM
Application Videos
-
Irrational Numbers
The video explains how to prove that a number is irrational.
-
Rational and Irrational Numbers
The video explains an example based on the concept of Rational and Irrat...
Concept Videos
-
Rational and Irrational Numbers
Discuss rational and irrational numbers and express them on the number lin... -
Rational and Irrational Numbers
Discuss rational and irrational numbers and express them on the number lin... -
Rational and Irrational Numbers
Discuss rational and irrational numbers and express them on the number lin...
CBSE 10 - Maths
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by reddyjaswamth | 10 Jan, 2024, 01:49: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by pv925403 | 07 Jan, 2024, 07:32: PM
ANSWERED BY EXPERT
CBSE 10 - Maths
Asked by abdulqadirmohd028 | 22 Dec, 2023, 12:56: AM
ANSWERED BY EXPERT
CBSE 10 - Maths
Asked by appanaboinakhasim8 | 05 Dec, 2023, 07:01: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by kanchandevi5268 | 03 Nov, 2023, 06:35: AM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by appusingh0840 | 29 Oct, 2023, 01:14: PM
ANSWERED BY EXPERTCBSE 10 - Maths
Asked by jilsmendapara123 | 28 Jul, 2023, 02:44: PM
ANSWERED BY EXPERT
