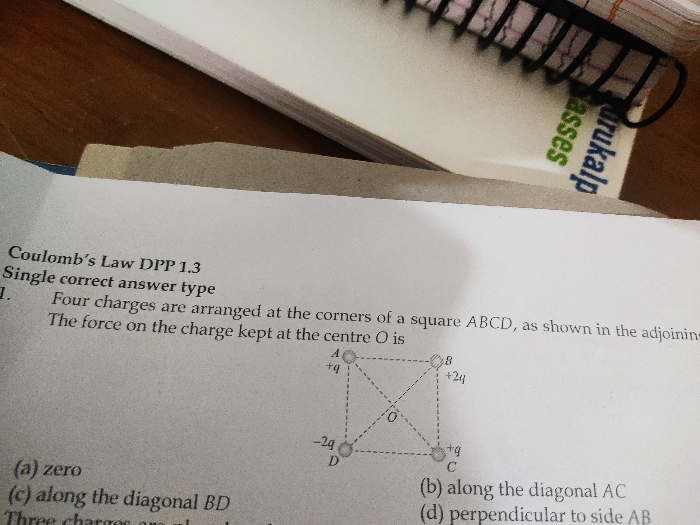JEE Class main Answered
Please solve the question

Asked by anshuman.anshuman090 | 30 Oct, 2019, 12:24: PM
To get the velocity of charge at surface of charged sphere, we equate the change in potential energy of charge from point P
to a point at surface of spher to change in kinetic energy of charge from point P to the point on the surface of sphere.
change in potential energy ΔU is given by
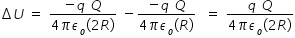 .............................(1)
.............................(1)hence velocity at a point on surface of charged sphere :- ΔU = (1/2)mv2 or velociy 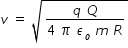
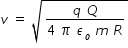
---------------------------------------------------------------
Change in potential from a point on surface of charged sphere to centre of sphere is calculated as follows
Electric field Er = - [ qQ / (4πεo) ] ( r/R3)
potential difference 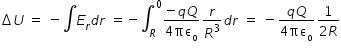
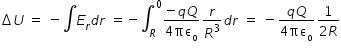
Hence if we equate change in potential energy to change in kinetic energy
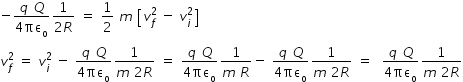
Hence velocity of charge at centre ,
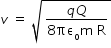
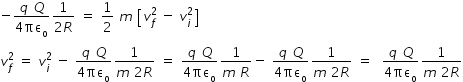
Answered by Thiyagarajan K | 01 Nov, 2019, 01:48: PM
Application Videos
JEE main - Physics
Asked by medhamahesh007 | 02 Apr, 2024, 11:11: AM
JEE main - Physics
Asked by gundlasumathi93 | 31 Mar, 2024, 02:13: PM
JEE main - Physics
Asked by chhayasharma9494 | 31 Mar, 2024, 12:47: PM
JEE main - Physics
Asked by archithateja3 | 30 Mar, 2024, 10:23: PM
JEE main - Physics
Asked by Machinenineha | 27 Mar, 2024, 05:28: PM
JEE main - Physics
Asked by mfkatagi099 | 20 Mar, 2024, 09:35: PM
JEE main - Physics
Asked by sreelekhachakali2006 | 15 Mar, 2024, 10:35: AM