CBSE Class 12-science Answered
Please give a detailed answer to this question .

Asked by Varsneya Srinivas | 25 Oct, 2017, 08:51: PM
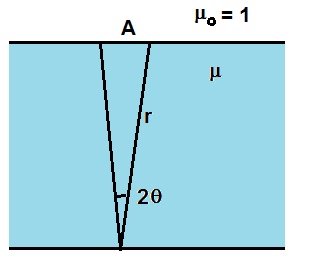
Due to total internal reflection light from point source escapes only through area A as illustrated in the first figure.
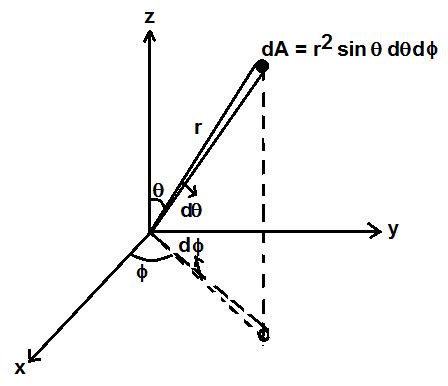
The circular area has to be calculated in spherical coordinates as shown in figure 2 by integrating the small area dA subtended by small solid angle dΩ.

Here θC is the critical angle for total internal reflection and is given by

Fraction of energy escape is the fraction of area A to the total spherical area 4πr2

Answered by | 11 Dec, 2017, 06:45: PM
Concept Videos
CBSE 12-science - Physics
Asked by mazhartahsildar143 | 07 May, 2020, 01:44: PM
CBSE 12-science - Physics
Asked by Hemanthrakshitha95 | 03 Mar, 2020, 02:55: PM
CBSE 12-science - Physics
Asked by rohitraman1115 | 08 Jan, 2019, 04:33: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 21 May, 2014, 09:18: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 21 May, 2014, 09:41: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 19 May, 2014, 04:38: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 12-science - Physics
Asked by Topperlearning User | 21 May, 2014, 09:49: AM
CBSE 12-science - Physics
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM




