NEET Class neet Answered

please answer this

Asked by Prashant DIGHE | 06 Dec, 2019, 10:31: PM

Expert Answer

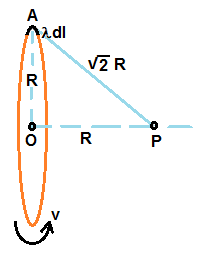
Figure shows a charged ring of radius R rotating with linear speed about axis OP.

Let a charge q is distributed uniformly, so that the ring has linear charge density λ per unit length.

Let us consider a small element of length dl at A. Electroc fileld dE at P due to this element of length dl is given by

dE = ( λ dl ) / [ (4πε_o) 2R² ]

Direction of this field is along the direction of line AP. The component resolved along the line OP is dE cos45 .

Hence electric field in the direction of line OP is given by, dE = (1/√2 ) ( λ dl ) / [ (4πε_o) 2R² ] .............(1)

electric field E in the direction of line OP due to full ring is obtained by integrating eqn.(1) through whole length of ring

E = (1/√2 ) ( λ 2πR ) / [ (4πε_o) 2R² ] = [1/( 2√2 )] { q / [ (4πε_o) 2R² ] } ....................(2)

magnetic field at P due to rotation of charged ring is calculated as follows.

Equivalent current of rotating charged ring = charge passing through the cross section of wire per unit time

Equivalent current i = q / [ (2πR)/v ] = λv.................(3)

Magnetic field dB by Biot_Severt's law at P due to line element dl is given by,

dB = [ ( μ_o/4π) i dl sin 45 ]/ ( 2R² ) ...........................(4)

Magenetic flux density due to whole ring is obtained by integrating eqn.(4)

B = (1/2√2) [ ( μ_o/4π) λv 2πR ]/ ( R² ) = (1/2√2) [ ( μ_o/4π) q v ]/ ( R² ) ..........................(5)

Substitution for current is done in the above equation using eqn.(3)

from eqn.(2) and (5) , we get the ratio of electric field to magnetic flux density is given by

( E / B ) = 1 / ( μ_o ε_o v ) = c² / v

Answered by Thiyagarajan K | 08 Dec, 2019, 02:08: PM

Application Videos