NEET Class neet Answered

please answer this

Asked by Prashant DIGHE | 18 Apr, 2020, 09:37: PM

Expert Answer

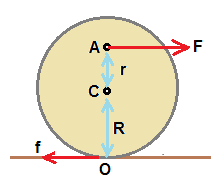
Let r be the distance from centre of mass to point A , which is point of application of force F .

Friction force f is acting at the point of contact.

Acceleration of centre of mass , a_C = ( F - f ) / M .....................(1)

where M is mass of rolling object

Angular acceleration is due to torque of applied force F and friction force f.

By taking point of contact as reference point, F(r+R) = I α = ( I_C + MR² ) α .........................(2)

where I is moment of inertia about point of contact O and it is given by, I = I_C + MR²

where I_C is moment of inertia about centre of mass.

Angular acceleration α = ( a_C / R ) ..............................(3)

By substituting angular acceleration using eqn.(3) in eqn.(2) and after simplification of eqn.(2),

we get the following equation for a_C

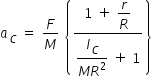begin mathsize 14px style a subscript C space equals space F over M space open curly brackets fraction numerator 1 space plus space begin display style r over R end style over denominator begin display style fraction numerator I subscript C over denominator M R squared end fraction end style space plus space 1 end fraction close curly brackets end style

............................(4)

From eqn.(1), we write friction force as , f = F - ( M a_C ) ....................(5)

Substituting for a_C using eqn.(4), we get friction force f from eqn.(5) as

begin mathsize 14px style f space equals F space open curly brackets fraction numerator I subscript C minus space M space R space r over denominator I subscript C plus space M space R squared end fraction close curly brackets end style

.................... (6)

Equation (4) and (6) helps us to know about movement of centre of mass and direction of friction force

(1) when force F is applied above centre, r is +ve

From eqn.(4), we know that the Rolling object moves forward

If the distance r satisfies the condition r < [ I_C / ( MR ) ], then from eqn.(6) we know that friction is backward

If the distance r is such that, r > [ I_C / ( MR ) ], then friction is forward

(2) when force F is applied at centre of mass, r is zero .

From eqn.(4), we know that the Rolling object moves forward

From eqn.(6) we know that friction is backward

(3) When force F is applied below centre of mass

From eqn.(4), we know that the rolling object moves forward

From eqn.(6) we know that friction is always backward

Answered by Thiyagarajan K | 20 Apr, 2020, 08:09: AM

Application Videos