NEET Class neet Answered

moment of inertia of a solid cylinder along an axis perpendicular to the axis of cylinder, we use parellel axis therom but i feel its wrong because the it can be applied only of the parellel axis pass through centre of mass of cylinder? can u please explain

Asked by bhupinderpal61 | 10 Oct, 2019, 12:21: PM

Expert Answer

Parallel axis theorem

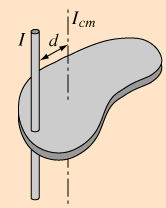
The moment of inertia of any object about an axis through its center of mass is the

minimum moment of inertia for an axis in that direction in space.

The moment of inertia about any axis parallel to that axis through the center of mass is given by

I_{parallel-axis} = I_CM + Md²

Your confusion is which axis is passing through centre of mass ?

Correct answer is reference axis is passing through centre of mass .

Using this reference axis passing through centre of mass, we are finding the moment of inertia about another parallel axis.

Hence parallel axis is not passing through centre of mass.

Moment of inertia of cylinder about an axis perpendicular to the axis of cylinder and passing through centre of mass is given below

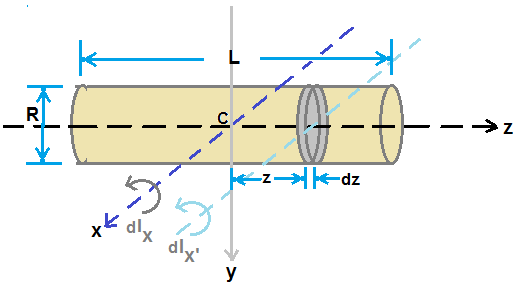
Let us consider a cylinder of radius R and length L and M be its mass.

Let the axis of cylinder coincides with z-axis of coordinate system.

We need to get moment of inertia about an axis perpendicular to axis of cylinder and passing throuh centre of mass of cylinder.

X-axis of coordinate system is the required axis of rotation as shown in figure.

Let us consider a thin disc of mass dm and thickness dz at a distance z frm centre of mass.

moment of inertia of this thin disk about axis of cylinder is given by

dI_z = (1/2) dm R² ..............(1)

By perpendicular axis theorem, dI_z = dI_x' + dI_y' .............(2)

where x', y' axis are mutually perpendicular axis to z-axis . By symmetry, dI_x' = dI_y'

Hence dI_x' = (1/2) dI_z = (1/4) dm R² ....................(3)

Moment of inertia given by above eqn. (3) is about the axis passing through centre of mass of thin disc.

Hence by parallel axis theorem, moment of inertia of this thin disc about the x-axis is given by

dI_x= (1/4) dmR² + dm z²................(4)

if mass is uniformly distributed, we have , dm = (M/L)dz ..............(5)

using eqn.(5), eqn.(4) is rewritten as, dI_x = (1/4)R²(M/L)dz + (M/L) z² dz ..............(6)

Moment of inertia of whole cylinder about the x-axis is given by

begin mathsize 14px style R squared over 4 open parentheses M over L close parentheses space integral subscript 0 superscript L d z space plus space open parentheses M over L close parentheses space integral subscript 0 superscript L z squared d z space space equals space 1 fourth M space R to the power of 2 space end exponent space plus space 1 third M space L squared end style

Answered by Thiyagarajan K | 12 Oct, 2019, 11:51: AM

NEET Class neet Answered

Application Videos

Growth of Current in L-R Circuit

CALL US / WHATSAPP

Please Login or Sign up to continue!

NEET Class neet Answered

Application Videos

Growth of Current in L-R Circuit

Choose Filters

Open In Ask A Doubt App ?

Get in Touch

Call / Whats App