ICSE Class 10 Answered
In triangle ABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that (i)CB : BA= CP:PA, (II) AB X BC = BP X CA.
Asked by Sushanta | 24 Mar, 2017, 07:51: PM
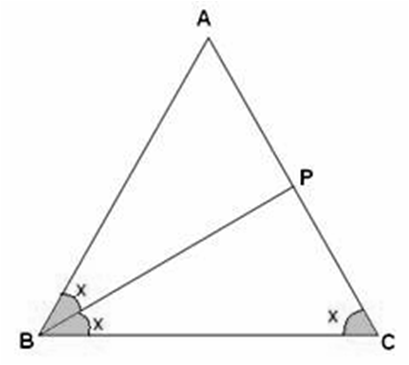
1) In ΔABC, ∠ABC = 2∠ACB
Let ∠ACB = x
⇒∠ABC = 2∠ACB = 2x
Given BP is bisector of ∠ABC
Hence ∠ABP = ∠PBC = x
Using the angle bisector theorem, that is,
Let ∠ACB = x
⇒∠ABC = 2∠ACB = 2x
Given BP is bisector of ∠ABC
Hence ∠ABP = ∠PBC = x
Using the angle bisector theorem, that is,
the bisector of an angle divides the side opposite to it in the ratio of other two sides.
Hence, CB : BA= CP:PA.
2) Consider ΔABC and ΔAPB
∠ABC = ∠APB [Exterior angle property]
∠BCP = ∠ABP [Given]
∴ ΔABC ≈ ΔAPB [AA criterion]
∴ [Corresponding sides of similar triangles are proportional.]
[Corresponding sides of similar triangles are proportional.]
⇒ AB x BC = BP x CA
Hence, CB : BA= CP:PA.
2) Consider ΔABC and ΔAPB
∠ABC = ∠APB [Exterior angle property]
∠BCP = ∠ABP [Given]
∴ ΔABC ≈ ΔAPB [AA criterion]
∴
 [Corresponding sides of similar triangles are proportional.]
[Corresponding sides of similar triangles are proportional.]⇒ AB x BC = BP x CA
Answered by Rebecca Fernandes | 24 Mar, 2017, 10:27: PM
Application Videos
Concept Videos
ICSE 10 - Maths
Asked by ahaana10065 | 28 Jul, 2020, 11:15: AM
ICSE 10 - Maths
Asked by saniyasadaf2008 | 30 May, 2020, 04:22: PM
ICSE 10 - Maths
Asked by moharchat8 | 07 Mar, 2020, 09:10: AM
ICSE 10 - Maths
Asked by hrmeenal24 | 14 Feb, 2020, 06:50: AM
ICSE 10 - Maths
Asked by latapranav | 22 Oct, 2019, 01:38: PM
ICSE 10 - Maths
Asked by jyotisethia97 | 17 Sep, 2018, 02:29: PM
ICSE 10 - Maths
Asked by dibyamrao000 | 11 May, 2018, 08:18: PM
ICSE 10 - Maths
Asked by lovemaan5500 | 14 Jan, 2018, 01:45: PM







 UTR ~
UTR ~