CBSE Class 9 Answered
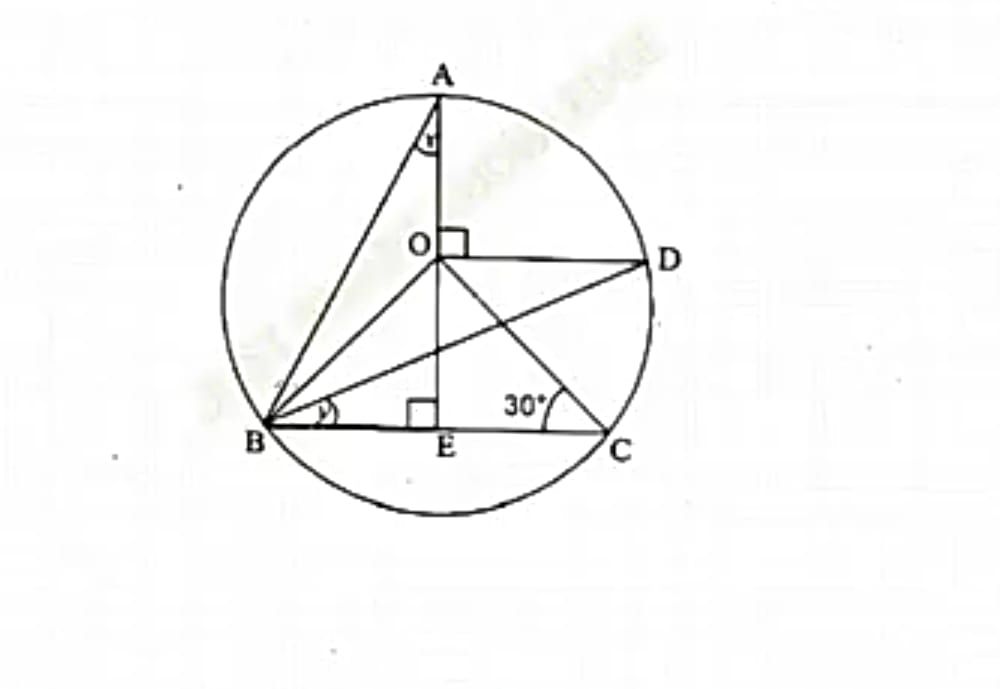
In the figure, PQ is a diameter of the
circle and XY is chord equal to the radius of the circle. PX and QY when
extended intersect at point E. Prove that 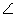 PEQ = 60o
PEQ = 60o


Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
PQ is the diameter of the circle, chord XY = r (radius of circle)
PX and QY extended intersect at a point E.
To
prove ![]() PEQ = 60o
PEQ = 60o
XY = OX = OY [radii of a circle, Given]
![]() XOY
is an equilateral triangle
XOY
is an equilateral triangle
![]()
![]()
![]() XQY
= 30o [Inscribed angle is
half of the central angle]
XQY
= 30o [Inscribed angle is
half of the central angle]
![]() PXQ = 90o [Angle in a semi circle]
PXQ = 90o [Angle in a semi circle]
![]()
![]() QXE = 180o -
QXE = 180o - ![]() PXQ = 900 [Linear pair]
PXQ = 900 [Linear pair]
In
![]() XEQ,
XEQ,
![]() XEQ
= 180o - (
XEQ
= 180o - (![]() EXQ +
EXQ + ![]() EQX) (Angle
sum property)
EQX) (Angle
sum property)
![]() XEQ = 180o - (900 + 300)
= 600
XEQ = 180o - (900 + 300)
= 600
![]()
![]() PEQ = 60o
PEQ = 60o
Answered by | 04 Jun, 2014, 03:23: PM
Concept Videos
CBSE 9 - Maths
Asked by geetaradha8835 | 16 Dec, 2022, 07:59: PM
CBSE 9 - Maths
Asked by sangeetabharti123456789 | 22 Feb, 2022, 09:01: AM
CBSE 9 - Maths
Asked by Samidhaindulkar133 | 11 Mar, 2021, 04:03: PM
CBSE 9 - Maths
Asked by harjot.arshleen | 03 Feb, 2021, 02:42: PM
CBSE 9 - Maths
Asked by lata15121995joshi | 03 Jan, 2020, 07:59: AM
CBSE 9 - Maths
Asked by Anubhavjain599 | 26 Nov, 2019, 05:53: PM
CBSE 9 - Maths
Asked by yogeshthakur3300 | 28 Dec, 2018, 08:24: AM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 9 - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM