ICSE Class 7 Answered
In a sample of 200 people, 150 liked tea, 75 liked coffee and 11 liked neither. How many people liked both tea and coffee?
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
Expert Answer
Let U = the no. of people sampled = 200 = the universal set.
T = no. of people who liked tea = 150
C = no. of people who liked coffee = 75
n (T 
C)' = 11 = no. of people who liked neither tea or coffee.
We have to find out how many people like both tea and coffee, i.e. n (T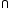 
C)
Now, n (T C) = n (U) - n (T C)' = 200 - 11 = 189
We know that
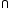n (T C) = n (T) + n (C) - n (T C)
Hence,
n (T 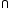C) = n (T) + n (C) - n (T C)
= 150 + 75 - 189 = 225 -189
= 36
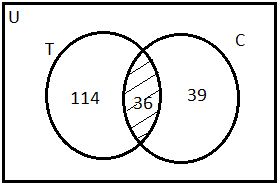
The following can also be showed using the venn diagram as below,
n (T 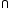C) is shown by the shaded region
Hence, 36 people like both tea and coffee.
Answered by | 04 Jun, 2014, 03:23: PM
