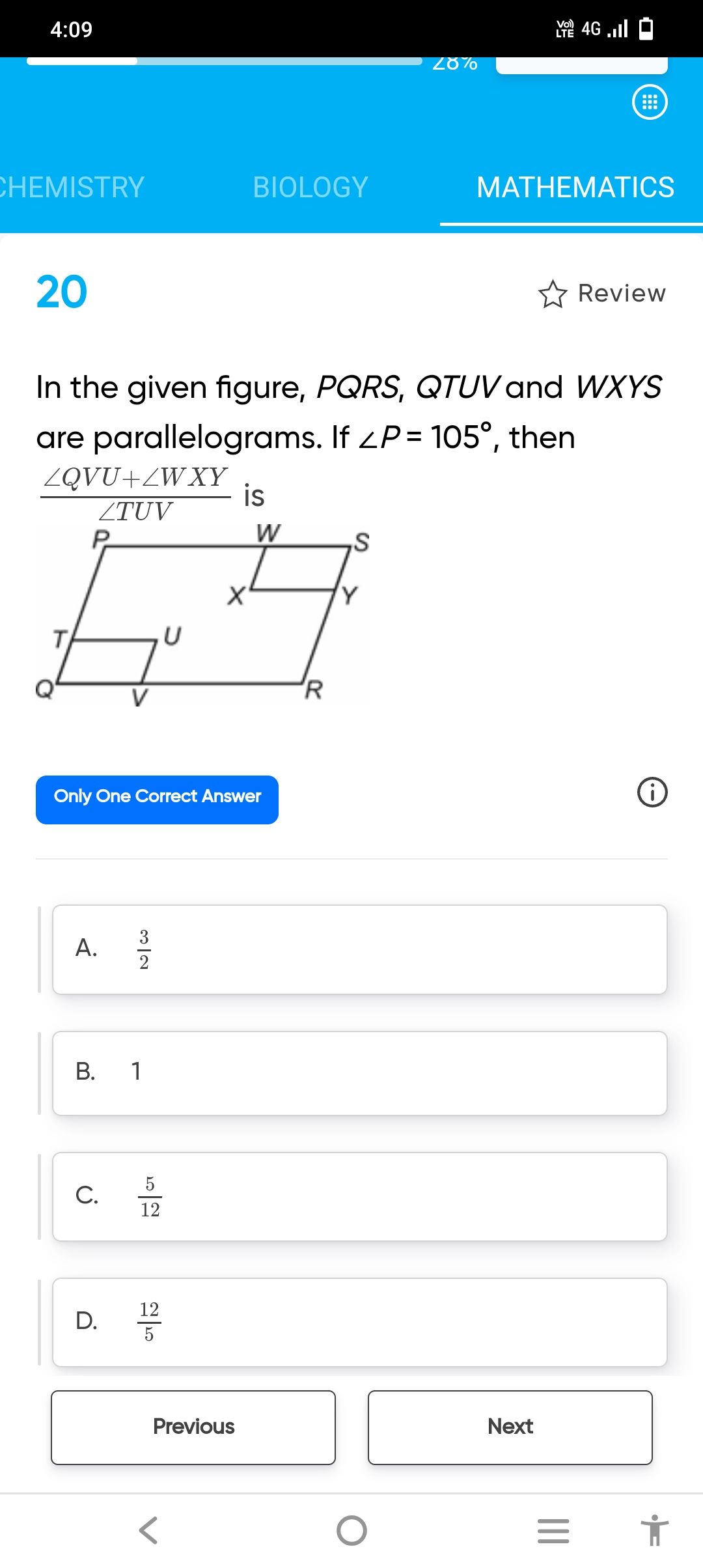
CBSE Class 9 Answered
if two opposite sides of a cyclic quadrilateral are parallel then prove that remaining two sides are equal and both the diagonals are equal
Asked by | 12 Mar, 2013, 10:41: PM
Let ABCD be the cyclic quadrilateral with AD parallel to BC. The center of the circle is O.
Join AC
Now, since AD is parallel to BC and AC is the transverse
angle DAC = angle ACB (interior opposite angles)
angle DAC is subtended by chord DC on the circumference and angle ACB is subtended by chord AB.
If the angles subtended by 2 chords on the circumference of the circle are equal, then the lengths of the chords is also equal.
Hence, DC = AB i.e. the 2 remaining sides of the cyclic quadrilateral are equal.
Now, BD and AC are the 2 diagonals.
In triangle ABD and triangle DCA
AB = CD (proved above)
angle DCA = angle DAB (angles subtended by the same chord AD)
angle ACB = angle DAC(proved above)
Hence, triangle ABD is congruent to triangle DCA (by ASA)
hence, BD = AC (by CPCT)
Answered by | 13 Mar, 2013, 01:15: AM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by chandininayak86 | 15 Dec, 2023, 07:36: AM
CBSE 9 - Maths
Asked by sagrawal0081 | 31 Aug, 2023, 07:24: PM
CBSE 9 - Maths
Asked by jahnavinehra | 03 Jul, 2022, 11:19: AM
CBSE 9 - Maths
Asked by seemarana8535 | 11 May, 2022, 04:17: PM
CBSE 9 - Maths
Asked by abhiroy1462 | 16 Apr, 2022, 02:25: PM
CBSE 9 - Maths
Asked by abdullahzedane2008 | 28 Mar, 2022, 12:11: PM
CBSE 9 - Maths
Asked by sanskritiraghudev | 19 Feb, 2022, 09:38: AM
CBSE 9 - Maths
Asked by varundhawan | 31 Jan, 2022, 10:41: PM
CBSE 9 - Maths
Asked by aziznoorani17 | 04 Jan, 2022, 11:32: AM
CBSE 9 - Maths
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM