CBSE Class 9 Answered
If there are three or more parallel lines
and the intercepts made by them on one transversal are equal, then the
corresponding intercepts by any other transversal are also equal.
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
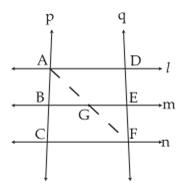
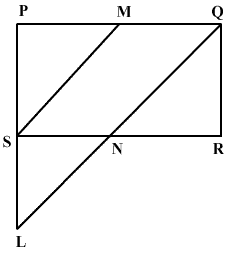
Given: l, m and n are three parallel lines intersected by transversals p and q such that l, m and n cut off equal intercepts AB and BC on p.
To prove: l, m and n cut off equal intercept DE and EF on q also.
Proof:
Join AF, suppose it intersect line m at G In ![]() ACF, B is the mid-point AC [
ACF, B is the mid-point AC [![]() AB = BC]
AB = BC]
And BG||CF
![]() G is the mid-point of AF [Converse of mid point theorem]
G is the mid-point of AF [Converse of mid point theorem]
In
![]() AFD, G is the mid point of AF and GE||AD
AFD, G is the mid point of AF and GE||AD
![]() E is the mid point of DF
E is the mid point of DF
![]() DE = EF
DE = EF
Hence l, m and n cut off equal intercepts DE and EF on q.
Answered by | 04 Jun, 2014, 03:23: PM
Application Videos
Concept Videos
CBSE 9 - Maths
Asked by vineetyadav77050 | 25 Jul, 2021, 05:45: PM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 11:58: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 12:01: PM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 11:59: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 12:00: PM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 12:00: PM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 11:52: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 11:56: AM
CBSE 9 - Maths
Asked by Topperlearning User | 11 Aug, 2017, 11:59: AM