CBSE Class 11-science Answered
If the lines 3x - 5y + 3 = 0, 5x + 7y - k = 0 and 2x - 3y - 5 = 0 are concurrent, find the value of k.
Asked by Topperlearning User | 30 Apr, 2014, 08:14: AM
Lines are said to be concurrent, if they pass through a common point, i.e., point of intersection of any two lines lies on the other line. Here given three lines are
3x - 5y + 3 = 0 --- (i)
5x + 7y - k = 0 ---(ii)
And 2x - 3y- 5 = 0 --- (iii)
Solving equation (i) and (iii), we get
x = 34 and y = 21.
Therefore, the point of intersection of two lines (i) and (iii) is (34, 21).
Since above three lines are concurrent, the point (34, 21) will satisfy equation (ii) so that
5 x 34 + 7 x 21- k = 0
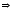 170 + 147 - k = 0
170 + 147 - k = 0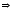 k = 317.
k = 317.
Answered by | 30 Apr, 2014, 10:14: AM
Application Videos
Concept Videos
CBSE 11-science - Maths
Asked by raistar7042 | 02 Dec, 2023, 01:22: PM
CBSE 11-science - Maths
Asked by priteshpatidar2525 | 17 Oct, 2023, 05:43: PM
CBSE 11-science - Maths
Asked by shahyogini5 | 31 Mar, 2023, 04:48: PM
CBSE 11-science - Maths
Asked by rekhavarma359 | 30 Apr, 2022, 03:00: PM
CBSE 11-science - Maths
Asked by prachifauzdar1 | 04 Jan, 2021, 12:18: PM
CBSE 11-science - Maths
Asked by Jayanthib615 | 31 Aug, 2020, 03:18: PM
CBSE 11-science - Maths
Asked by kumarisakshi0209 | 22 Aug, 2019, 08:11: PM
CBSE 11-science - Maths
Asked by kumarisakshi0209 | 21 Aug, 2019, 08:59: PM
CBSE 11-science - Maths
Asked by khushipattidar595 | 05 Nov, 2018, 08:48: AM
CBSE 11-science - Maths
Asked by lovemaan5500 | 07 Oct, 2018, 12:16: PM







