CBSE Class 10 Answered

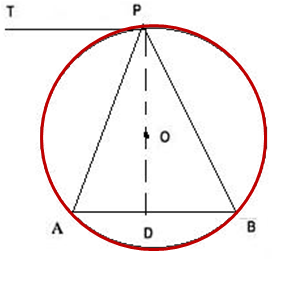
Construction: Join PO and produce it to D.

Now, OP is perpendicular TP  (tangent makes a 90° angle with the radius of the circle at the point of contact)

Also, TP is parallel to AB (given)

angle ADP = 90° (interior angles)

So, OD is perpendicular to AB.

Since, a perpendicular drawn from the center of the circle to a chord bisects it,

PD is a bisector of AB. i.e. AD = DB

Now in triangle ADP and BDP

AB = DB (proved above) 

angle ADP = angle BDP (both are 90°)

 PD = DP  (common)

Triangle ADP Triangle BDP (By SAS congruence criterion)

Hence, angle PAD = angle PBD (By CPCT)

Thus, APB is an isosceles triangle.