CBSE Class 11-science Answered
If p and q are the lengths of perpendicular from the origin to the lines x cos q - y sin q = k cos 2 q and x sec q + y cosec q = k respectively. Prove that p2 + 4q2 = k2.
Asked by Topperlearning User | 30 Apr, 2014, 09:08: AM
The perpendicular distance from the origin to the line
x cos q - y sin q = k cos 2 q ... (i)
Now,
x sec q + y cosec q = k
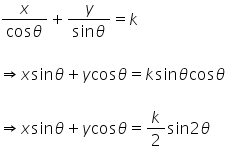
The perpendicular distance q from the origin to the line (ii)

Answered by | 30 Apr, 2014, 11:08: AM
Concept Videos
CBSE 11-science - Maths
Asked by Topperlearning User | 04 Jun, 2014, 01:23: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 20 Oct, 2016, 06:34: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 29 Apr, 2014, 03:09: PM
CBSE 11-science - Maths
Asked by Topperlearning User | 20 Oct, 2016, 06:32: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 28 Apr, 2014, 08:04: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 09:00: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 09:03: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 30 Apr, 2014, 09:08: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 20 Oct, 2016, 06:26: AM
CBSE 11-science - Maths
Asked by Topperlearning User | 20 Oct, 2016, 06:20: AM



 5y + 23 = 0 and passing through the point (3, -5).
5y + 23 = 0 and passing through the point (3, -5).