Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

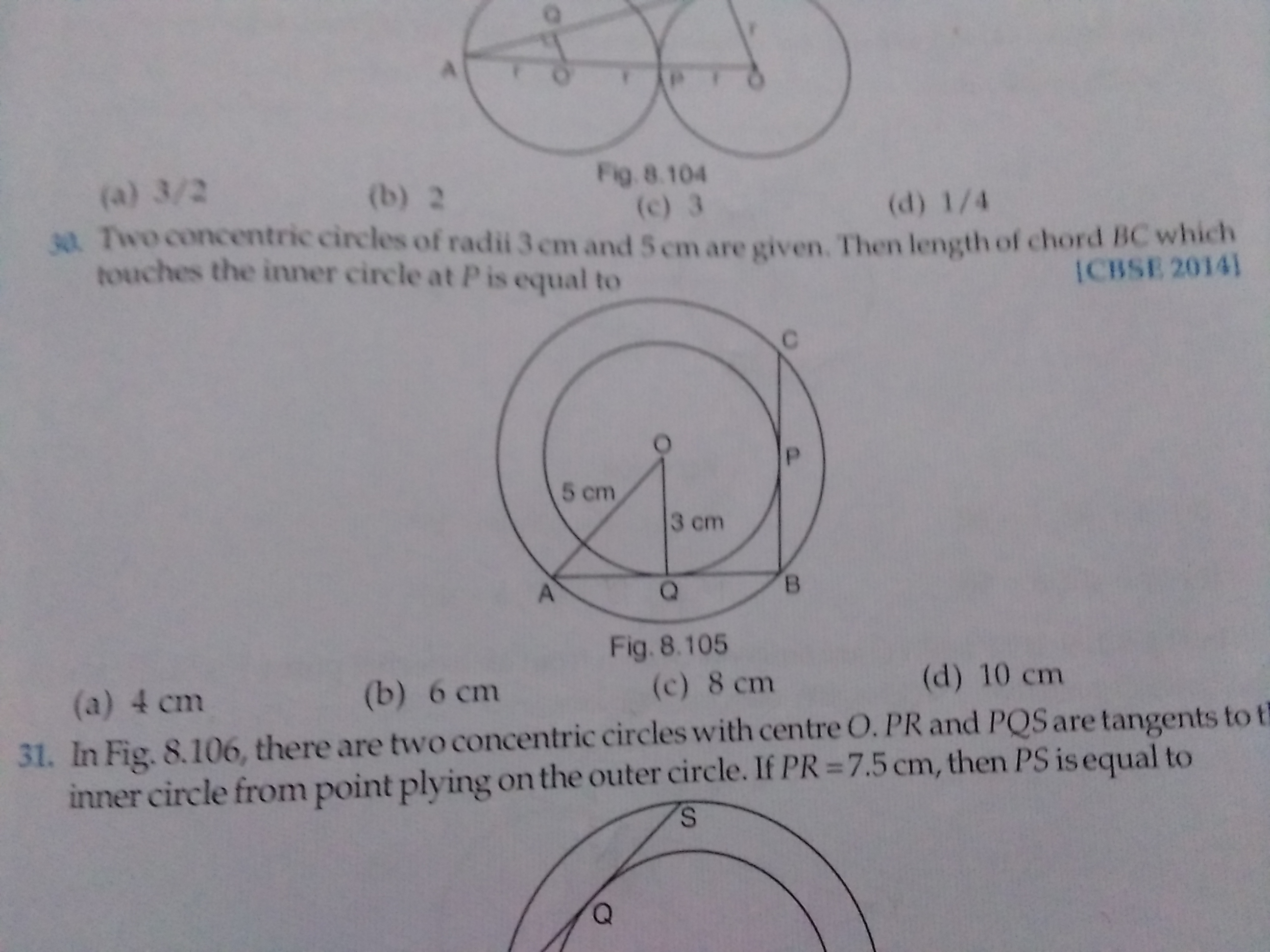
If d1, d2(d2>d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, prove that d2^2 = d1^2 + c^2
Asked by Ritwika Sharma | 12 Mar, 2013, 08:53: PM
answered-by-expert Expert Answer
Answer: Given :  d1, d2 (d2>d1) be the diameters of two concentric circles and C be the lengths of a chord of a circle which is tangent to the other circle
To prove : d2= d1 2 + C2
 
Now
OQ = d2/2 , OR = d1/2 and PQ=c
Since PQ istangent to the circle 
therefore OR is perpendicular to PQ
=> QR = PQ/2 = c/2
 
Using pythagorus theorm in triangle OQR
OQ2 = OR2 + QR2
=> (d2 /2)2 = (d1/2)2 + (c/2)2
=>1/4 (d2)2 = 1/4 (d1)2 +(c)2
=> d22 = d12 +c2
Hence Proved
Answered by | 12 Mar, 2013, 11:50: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
PQ is a chord of length 8 cm to a circle of radius 5 cm. The tangents P and Q intersect at a point T. Find the length of the tangent TP.
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
in the given figure a triangle abc is drawn to circumscribe a circle of radius 3 cm such that the segment bd and dc are respectively of length 6 and 9 cm if the area of traingle abc is 54cm2 then find side ab and ac
question image
Asked by jennyy | 26 Mar, 2022, 08:41: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
3. Two supplementary angles are subtended at the centre by two arcs of a circle of radius 7 cm. Find the total length of these arcs  
Asked by sowmyashreeiyer | 31 Jan, 2022, 11:40: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
From a point P, two tangents PA and PB are drawn to a circle C(0, r).  If OP = 2r, then find ∠𝐴𝑃𝐵. What type of triangle is APB?  
Asked by riazu945 | 16 Jan, 2022, 01:00: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
in the above figure major
question image
Asked by ajabraosable27 | 11 Oct, 2021, 09:28: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prime factorisation
Asked by amikasangma080 | 11 Oct, 2021, 06:14: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact
Asked by muskanmahek2411 | 08 Oct, 2021, 10:48: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
radious of circle is
Asked by anishasheoran372 | 13 Jul, 2021, 09:33: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
In the adjoining figure, AB is the Diameter of the circle. E is not the centre. Angle ACD = 30°. Find angle x.
question image
Asked by bhilarevishwesh | 21 May, 2021, 08:27: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
Q30
question image
Asked by sangyaswarupa | 16 Mar, 2021, 10:06: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×