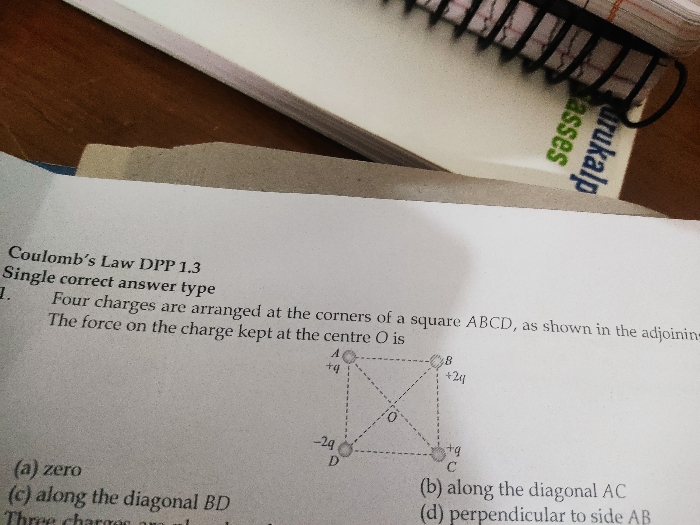JEE Class main Answered
If a heavy spring of uniform density and mass m is hung vertically so that it is stretched by gravity under its own weight, where is the center of mass?
Asked by rushabhjain.av | 20 Nov, 2019, 10:00: PM
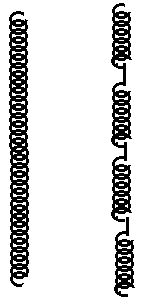
A heavy spring of mass M and length L can be considered as N number of springs connected in series,
each having length l and amss m so that
M = N × m .....................(1)
L = N × l .....................(2)
If each small spring has spring constant k, then the spring constant of heavy spring is K , so that K = k/N .
when the heavy spring is suspended vertically, extension of the spring due to gravity and its own mass is different for lower and upper parts of spring.
Upper part of spring due to heavy mass haging down below it , has more extension than the Lower part of spring.
Let us consider the extension of individual small spring :- F = m'g = k Δl' ...............(3)
where m' is the mass hanging below the spring and Δl' is the extension
Let Δl be the extension of each spring due to its own mass m.
Then we have , mg = k Δl or Δl = (mg)/k .........................(4)
Let us consider spring-1 is the top most small spring, spring-2 is next spring below it , so on.
Each spring's extension depends on the total mass of springs hanging below.
Let us consider the distance of centre of mass of each spring from top most hanging point.
Extended length of each small spring and distance of centre of mass of each extended spring is tabulated and it is given below
| Spring No. n | Extended Length |
Distance yn of centre of mass
of spring
|
| 1 | l + NΔl | (1/2) [ l + N Δl ] |
| 2 | l + (N-1)Δl | [ l + N Δl ] + [ l + (N-1)Δl ] /2 = (3/2) [ l + N Δl ] - (Δl/2) |
| 3 | l + (N-2)Δl | [ l + N Δl ] + [ l + (N-1)Δl ] + [ l + (N-2)Δl ] /2 = (5/2) [ l + N Δl ] - 2(Δl/2) |
| 4 | l + (N-3)Δl | l + N Δl ] + [ l + (N-1)Δl ] + [ l + (N-2)Δl ] + [ l + (N-3)Δl ] /2 = (7/2) [ l + N Δl ] - 3(Δl/2) |
| -------- | ------------- | -------------- |
| -------------- | ------------- | ---------------- |
| -------------- | ---------------- | ------------------ |
| N-1 | l + 2 Δl | ( (2N-3)/2 ) [ l + N Δl ] - (N-2)( Δl / 2 ) |
| N | l + Δl | ( (2N-1)/2 ) [ l + N Δl ] - (N-1)( Δl / 2 ) |
Let Y be the cenetre of mass when the heavy spring is suspended vertically and it extends due to its own mass.
Then by defineition of centre of mass,
Above summation is wroked out using values of tabulated yn as
M × Y = m N2 [ l + N Δl ]/2 + m [ (N-1)(N)/2 ] ( Δl / 2 )
when N -> ∞ , N(N-1) ≈ N2
Hence M × Y = m N2 [ (l/2) + ( N + (1/2)) Δl ]
since M = m × N , we get , Y = N [ (l/2) + ( N + (1/2)) (Δl/2) ]
we use N × l = L , where L is length of spring in the above equation.
Also we use the approximation when N -> ∞ , N [ N +(1/2) ] ≈ N2
Y = (L/2) + N2(Δl/2) = (L/2) + N2 (mg)/(2k) = (L/2) + (M g )/ ( 2 K )
( We have used, ( N m ) = M and (k/N) = K in the above equation )
Answered by Thiyagarajan K | 26 Nov, 2019, 11:24: AM
Application Videos
JEE main - Physics
Asked by ksahu8511 | 19 Apr, 2024, 11:55: AM
JEE main - Physics
Asked by mohammedimroz | 13 Apr, 2024, 09:48: PM
JEE main - Physics
Asked by medhamahesh007 | 02 Apr, 2024, 11:11: AM
JEE main - Physics
Asked by gundlasumathi93 | 31 Mar, 2024, 02:13: PM
JEE main - Physics
Asked by chhayasharma9494 | 31 Mar, 2024, 12:47: PM
JEE main - Physics
Asked by archithateja3 | 30 Mar, 2024, 10:23: PM
JEE main - Physics
Asked by Machinenineha | 27 Mar, 2024, 05:28: PM
JEE main - Physics
Asked by mfkatagi099 | 20 Mar, 2024, 09:35: PM