Please wait...
Contact Us
Contact
Need assistance? Contact us on below numbers

For Study plan details

93219 24448 / 89292 63204

10:00 AM to 7:00 PM IST all days.

For Franchisee Enquiry

81783 72169
OR

Chat with us on WhatsApp

or

Thanks, You will receive a call shortly.
Customer Support

You are very important to us

For any content/service related issues please contact on this number

93219 24448 / 99871 78554

Mon to Sat - 10 AM to 7 PM

Home / Doubts and Solutions/MAHARASHTRA OLD/Class 9/Mathematics

I WANT HOW TO KNOW ABOUT WHICH TEST OF SIMILARITY IS APPLICABLE FOR SOMES I M CONFUSED IN TEST OF SIMILARITY

Asked by ayushsingh1214 10th August 2016, 10:31 PM
Answered by Expert
Answer:
SSS similarity criterion:
The triangles shown are similar as their corresponding sides are proportional.
Example:
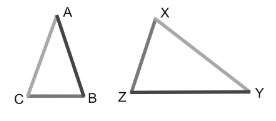
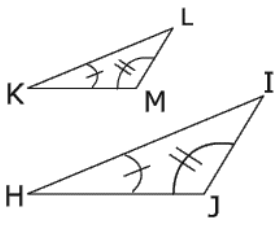
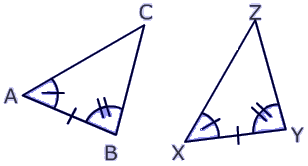
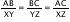So, when begin mathsize 8px style AB over XY equals BC over YZ equals AC over XZ end style that is the sides are proportional, then the triangles ABC and XYZ are similar.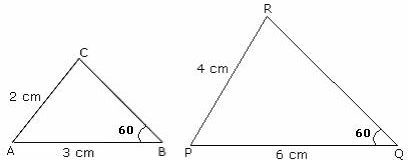
 
 
SAS similarity criterion:
The triangles shown are similar as their corresponding angle is congruent and the sides including this angle are proportional.
Example:
So, when two sides are given proportiional and the included angle between those sides are given equal, then the triangles are proportional, and we can use the SAS similarity criterion in this case.
 
AAA similarity criterion:
The triangles shown are similar as the corresponding angles of one triangle are equal to the corresponding angles of the other triangle.
Example:
 
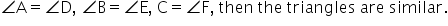
So, when angle straight A equals angle straight D comma space angle straight B equals angle straight E comma space straight C equals angle straight F comma space then space the space triangles space are space similar.
 
 
 
AA similarity criterion:
The triangles shown are similar as TWO of the corresponding angles of one triangle are equal to the TWO corresponding angles of the other triangle.
Example:
 
 
So, in this case two pairs of angles are equal, so, we can use the angle sum property to each triangle and obtain the third angle.
Then we can use the AAA similarity criterion.
 
 
ASA similarity criterion:
The triangles shown are similar as two of the corresponding angles of one triangle are equal to the two corresponding angles of the other triangle and the side included between these angles are equal.
Example:
 
So, in this case two pairs of angles are equal and the included sides are equal.
Answered by Expert 11th August 2016, 9:57 AM
Rate this answer
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10

You have rated this answer /10

Report an issue
Previous Question
Next Question
Your answer has been posted successfully!

Free related questions

RELATED STUDY RESOURCES :
MAHARASHTRA OLD Class-9 QUESTION ANSWERS

Chat with us on WhatsApp