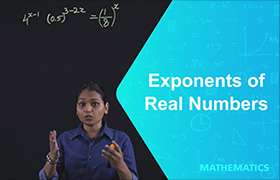Assume x=m/n where mbelongs to Z and nbelongs to N
this implies x=sqaure root(m)/ square root(n)
which means that for an integer to have a rational root it's root must be the ratio of two integer roots. For this ratio to not be an integer m and n must be distinct which implies that x is not an integer quantity.
From contradiction Hence Proved