CBSE Class 10 Answered
how to find the other two zeroes if two of them are already given for a 4 degree polynomial. example me with the help of an unique example. thanks
Asked by Lochan Khatri | 21 Sep, 2013, 04:53: PM
Suppose a and b are roots of a fourth degree polynomial.
Then, (x - a) and (x - b) will be the factors of the polynomial and hence, (x-a)(x-b) will be a factor of the polynomial.
Now, to find the other two factors, divide the polynomial with (x-a)(x-b) = x2 - x(a+b) + ab. You will get 0 as the remainder and the quotient will be a second degree polynomial.
By division algorithm,
p(x) = q(x) (x-a)(x-b)
Hence, the roots of q(x) will be the remaining two roots of the fourth degree polynomial.
Example: If two of the zeroes of the polynomial p(x) = 5x4 - 5x3 - 33x2 + 3x + 18 are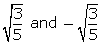 , find the other two zeroes.
, find the other two zeroes.
Solution:

Answered by | 22 Sep, 2013, 03:42: PM
Application Videos
Concept Videos
CBSE 10 - Maths
Asked by anubhutiupadhaya | 14 Mar, 2024, 11:57: AM
CBSE 10 - Maths
Asked by reetudetha | 08 Jan, 2024, 04:12: PM
CBSE 10 - Maths
Asked by mysticsurya201 | 04 Jan, 2024, 08:25: PM
CBSE 10 - Maths
Asked by fatehbahadurtiwari3 | 30 Dec, 2023, 06:25: PM
CBSE 10 - Maths
Asked by dhaneswarnimal80 | 11 Nov, 2023, 06:50: AM
CBSE 10 - Maths
Asked by skandachiranjeevin | 01 Nov, 2023, 08:58: PM
CBSE 10 - Maths
the value 'p'for which polynomials x²-(p²-9)x+8has zeroes equal in magnitude but opposite in sign is


Asked by sazimkhan178 | 16 Sep, 2023, 11:27: AM
CBSE 10 - Maths
Asked by pranavtamboli65 | 09 Jul, 2023, 09:13: PM
CBSE 10 - Maths
Asked by rekhapreetham | 15 Jun, 2023, 08:23: PM
CBSE 10 - Maths
Asked by dimpaldihingia2 | 24 May, 2023, 06:10: PM