Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 9 Answered

How can i prove that the medians of a triangle are concurrent for a class 9 standart?  
Asked by ishitahazarika.i22 | 13 Jan, 2019, 12:45: AM
answered-by-expert Expert Answer

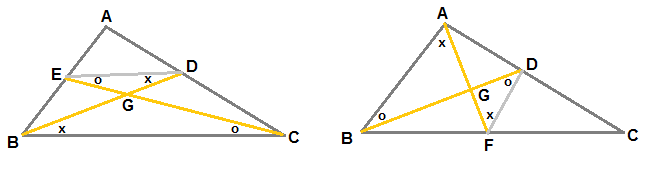
Let D and E are mid point of side AC and side AB respectively. Let us join D and E as shown in left side of figure.
We know that since D and E are mid points two sides of triangle, line DE is parallel to third side BC and DE = (1/2)BC.
 
Since DE is parallel to BC, as marked in the figure, begin mathsize 12px style angle end styleEDG = begin mathsize 12px style angle end styleGBC and begin mathsize 12px style angle end styleDEG = begin mathsize 12px style angle end styleGCB .
Hence ΔGED and ΔGBC are similar triangles. we have begin mathsize 12px style fraction numerator E D over denominator B C end fraction space equals space fraction numerator E G over denominator G C end fraction space equals fraction numerator D G over denominator G B end fraction equals 1 half end style
Hence the intersection point G divides the median BD and CE in the ratio 2:1  or GD = (1/3)BD  and GE = (1/3)CE
 
Now if we draw medians BD and AF as shown in right side of figure, we can similarly prove ΔGFD and ΔGAB are similar,
BD and AF intersects at G so that GF = (1/3)AF  and GD = (1/3)BD
 
since we have proved in both the cases,  if any two medians intersect, then intersection point divides the medians in the ratio 1:3,
hence all the three medians are concurrent
Answered by Thiyagarajan K | 14 Jan, 2019, 01:59: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 9 - Maths
13. If x = (2 + sqrt(3)) find the value of x ^ 2 + 1/(x ^ 2)
Asked by monika.vns14 | 18 Apr, 2024, 05:15: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
3√5+√3/√5-√3
Asked by gulshanelectronics2017 | 15 Apr, 2024, 05:35: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
find the value of n in 7^2n+1÷49=7^3
Asked by tripura78839 | 12 Apr, 2024, 09:05: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
how to solve it
question image
Asked by singhanjali0199 | 12 Apr, 2024, 08:29: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
√2x^2+3x+√2
question image
Asked by killerstealer593 | 11 Apr, 2024, 07:50: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
x²-22x+120
Asked by rson0295 | 01 Apr, 2024, 08:55: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
Draw the graph of the equation of line 2x + 3y = 6. Write the co ordinates of the point where the line intersects X-axis and Y-axis.
question image
Asked by saee.shinde3069 | 31 Mar, 2024, 10:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
locate √2 on number line
Asked by rathoreraj7296 | 31 Mar, 2024, 08:09: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
ab is diameter of circle with centre o . CD is a code equal to the radius of the circle a c and b b when extend intersect at the point e prove that angle a e b is equals to 60 degree
Asked by divyanshibirla037 | 29 Mar, 2024, 03:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 9 - Maths
5x=25 find x.
Asked by dhokwaltushar | 25 Mar, 2024, 04:26: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×