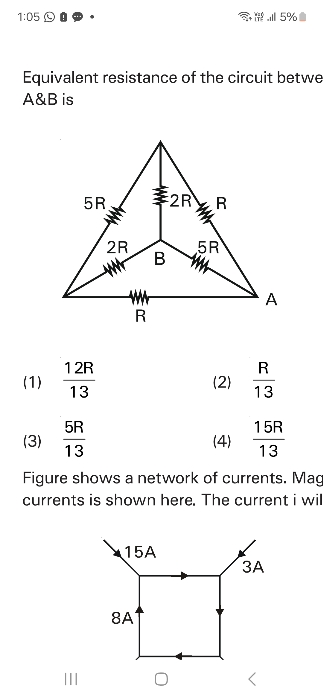
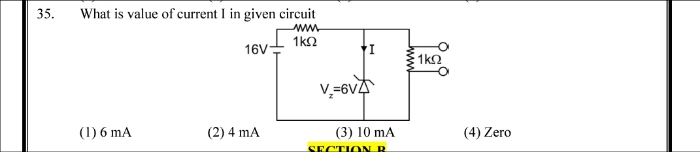
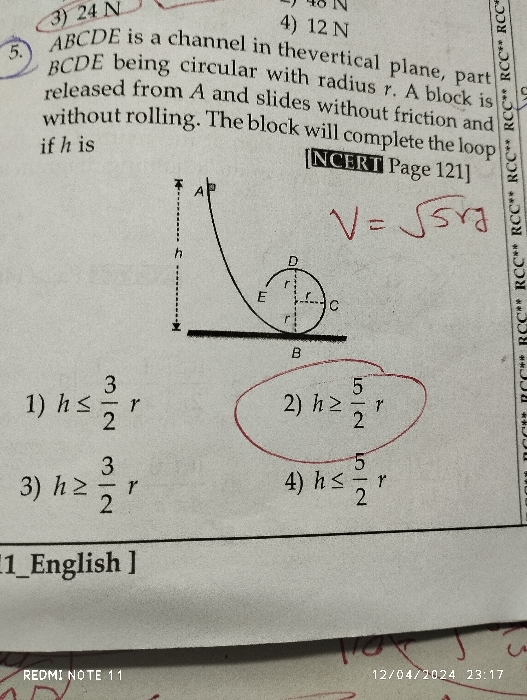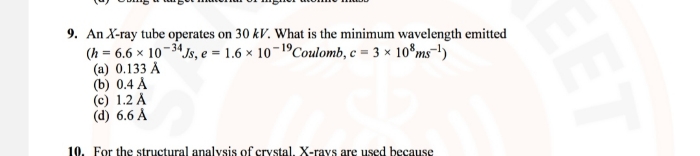NEET Class neet Answered

⭕ Help me in this question...Thanks☺️

Asked by jhajuhi19 | 23 Nov, 2019, 02:12: PM

Expert Answer

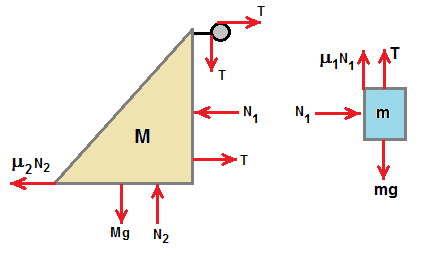
Figure given above shows the free body diagram (FBD) of bith blocks. Forces acting on each block are shown in FBD .

Let us consider the block of mass M. Mg is the weight , i.e. gravitational force of block,

N₂ is the reaction force acting beteen the contact surfaces of floor and block,

μ₂N₂ is the friction force acting against the movement of block .

T is tension force acting on the rope and aslo at pulley connected to block.

N₁ is the normal reaction force exerted by block of mass m

Now let us see FBD of block of mass m . Gravitationa forec, i.e. weight mg is acting downward, T is tension in the rope,

μ₁N₁ is the friction force acting against the movement along the contact surface between two blocks

and N₁ is the reaction force exerted by block of mass M.

Let us apply the Newtons second law for the block of mass m

In horizontal direction, if we assume a_x is acceleration of mass m , then we have, N₁ = m a_x .....................(1)

In vertical direction, if we assume a_y is acceletaion of mass m , then we have, mg - μ₁ N₁ - T = m a_y ...............(2)

Let us apply the Newtons second law for the block of mass M

In horizontal direction, if we assume A_xisthe acceleration of block of mass M,

then we have, 2T - N₁ - μ₂ N₂ = M A_x ...............(3)

In Vertical direction, there is no movement , hence we have, N₂ = M g + T ........................(4)

At equilibrium, we have, a_x = a_y = A_x = 0

Hence from eqn.(1), we get N₁ = 0

By using N₁= 0 and a_y= 0, from eqn.(2) we get, T = mg

By substituting for T, N₁, N₂ and A_x in eqn.(3) , we get , ( 2 m g ) - μ₂ ( M g + m g ) = 0

Hence , we get, m = ( μ₂ M ) / ( 2 - μ₂ ) = (0.4 × 20 ) / (2 - 0.4 ) = 5 kg

Answered by Thiyagarajan K | 23 Nov, 2019, 10:55: PM

Application Videos