Ask a Doubt
Request a call back

Join NOW to get access to exclusive study material for best results

CBSE Class 10 Answered

Find the sum of all natural numbers from 1 to 1000 which are neither divisible 2 nor by 5.
Asked by asumangalashetty | 13 Jan, 2019, 09:16: AM
answered-by-expert Expert Answer
Sum of all natural numbers 1 to 1000 = 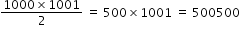begin mathsize 12px style fraction numerator 1000 cross times 1001 over denominator 2 end fraction space equals space 500 cross times 1001 space equals space 500500 end style 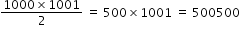................................(1)
even numbers from 2 to 1000 form  A.P with first term 2, common difference 2 and there are 500 terms in A.P
 
Hence sum of even numbers = 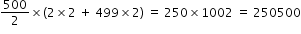begin mathsize 12px style 500 over 2 cross times open parentheses 2 cross times 2 space plus space 499 cross times 2 close parentheses space equals space 250 cross times 1002 space equals space 250500 end style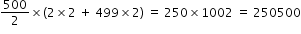................................(2)
Similarly numbers divisible by 5 which are occuring in the range 1 to 1000 forms A.P with first term 5, common difference 5 and there are 200 terms.
 
Hence sum of numbers that are divisible by 5 = 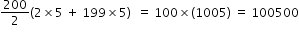begin mathsize 12px style 200 over 2 open parentheses 2 cross times 5 space plus space 199 cross times 5 close parentheses space space equals space 100 cross times open parentheses 1005 close parentheses space equals space 100500 end style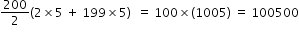..........................(3)
In the sum given by eqn.(3), there are some even numbers occuring also in the sum given by eqn.(2).
we have to exclude the sum of those numbers to get the required sum . 
 
These numbers are even and also divisible by 5,  hence they are divisible by 10, and forms A.P with first term 10, common difference 10
and there are 100 terms in A.P
Sum of the numbers that are divisible by 10  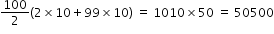= begin mathsize 12px style 100 over 2 open parentheses 2 cross times 10 plus 99 cross times 10 close parentheses space equals space 1010 cross times 50 space equals space 50500 end style 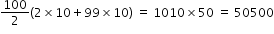........................(4)
Hence, using eqns.(1), (2), (3) and (4), sum of natural numbers from 1 to 1000,
which are not divisble by 2  and not divisible by 5  = 500500 - (250500 + 100500 - 50500) = 200000
Answered by Thiyagarajan K | 13 Jan, 2019, 10:13: PM

Application Videos

Concept Videos

Multiple Choice Questions Practice Test
Answered Unanswered My Questions My Answers
CBSE 10 - Maths
2/x+2/3y=1/6; 3/x+2/y=0
Asked by aditikaldate7 | 21 Apr, 2024, 03:16: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
ABCD is a rectangle in which diagonal AC is equals to 17 cm angle BCA is equals to thitha and sin theta is equals to 8/17 find the area of rectangle ABCDE (ii) the perimeter of rectangle ABCD
Asked by pathaksuman622 | 21 Apr, 2024, 11:56: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
PQ is a chord of length 8 cm to a circle of radius 5 cm. The tangents P and Q intersect at a point T. Find the length of the tangent TP.
Asked by yalagondanikhil | 16 Apr, 2024, 12:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
if one of the zeroes of quadratic polynomial F(x) = 4x² - 8kx - 9 is equal in magnitude but opposite in sign, find K
Asked by rrajansinghakb199 | 08 Apr, 2024, 05:12: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
express 15.265 in p/q form?
Asked by nagalaxmidurgarao937 | 08 Apr, 2024, 01:42: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
the poles AB and CD of different heights are standing vertically on the ground level from a point P on the line joining the foots of the pole on the level of ground the angle of elevation to the top of the pole are founded to be complementary the of the CD and the distance PD 20√3m and 20m respectively if the BP is 10m then find the length of AB and the distance AC between the tpo of the poles
Asked by mraniruddha03 | 02 Apr, 2024, 06:44: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
from the pair of linear equations in the following problems and find their solution graphically 10 students of class 10 to part in a mathematic quiz if the number of girls is for more than the number of boys find the number of boys and girls who took part in the quiz
Asked by muttenenimalleswarrao | 29 Mar, 2024, 08:32: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
maths
question image
Asked by sonawnerohan01 | 23 Mar, 2024, 12:25: PM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
The distance of the point (5,-2) from x-axis will be :-
Asked by pathakvaishnavi9139 | 23 Mar, 2024, 10:45: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
CBSE 10 - Maths
income of families locality are given. find the mode of the data (income in rupees)=1-200,201-400,401-600,601-800,801-1000 and number of families are 7,10,16,12,3
question image
Asked by mustafahssn786 | 23 Mar, 2024, 06:25: AM
ANSWERED BY EXPERT ANSWERED BY EXPERT
My Class Videos Tests ₹ Plans Ask a Doubt
Get Latest Study Material for Academic year 24-25 Click here
×