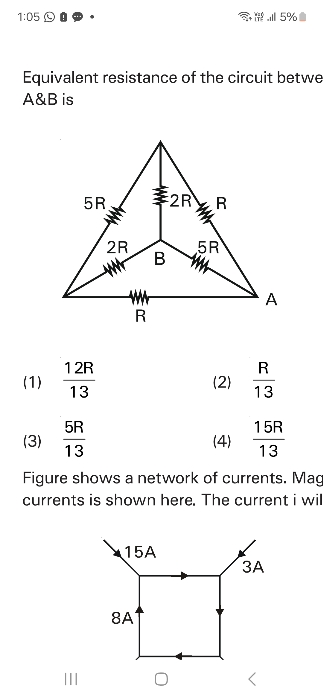
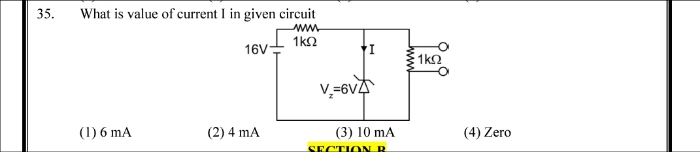
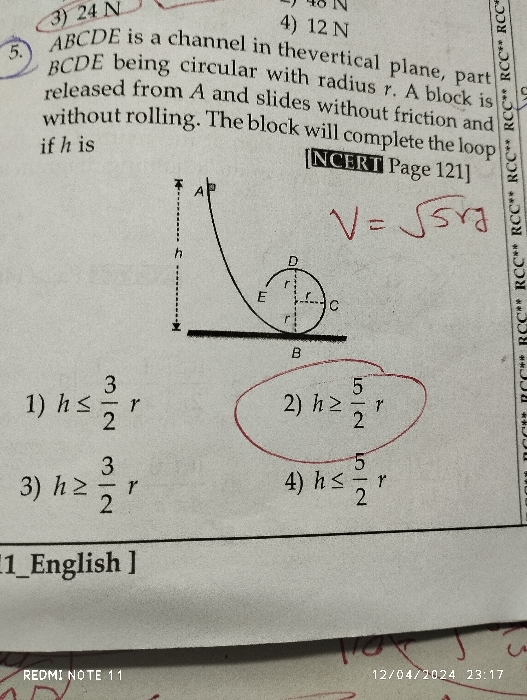NEET Class neet Answered

Find the position relative to the lens of the image of the object formed by the system. [ ans is 1]

Asked by Prashant DIGHE | 08 Jul, 2019, 05:49: PM

Expert Answer

First, let us find the radius of curvature R from given focal length 30 cm using lens makers formula.

1/f = ( μ_g - 1) [ (1/R)+(1/R) ]

1/30 = (1.5-1) (2/R) or R = 30 cm

at spherical surface of air-glass interface, we have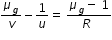

begin mathsize 12px style mu subscript g over v minus 1 over u equals space fraction numerator mu subscript g minus space 1 over denominator R space space end fraction end style

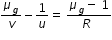......................(1)

where v is the first image distance at right side of lens, u is object distance at left side of lens

substituting the values in eqn.(1), (1.5/v) -(1/-90) = 0.5/30, we get v = 270 cm

Hence first image is formed at 270 cm from lens at right side.

This is acting as virtual object for spherical surface of glass-water interface

then we have ,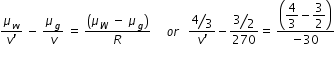

begin mathsize 12px style fraction numerator mu subscript w over denominator v apostrophe end fraction space minus space mu subscript g over v space equals space fraction numerator open parentheses mu subscript W space minus space mu subscript g close parentheses over denominator R end fraction space space space space space o r space space space fraction numerator begin display style bevelled 4 over 3 end style over denominator v apostrophe end fraction minus fraction numerator begin display style bevelled 3 over 2 end style over denominator 270 end fraction equals space fraction numerator open parentheses begin display style 4 over 3 end style minus begin display style 3 over 2 end style close parentheses over denominator negative 30 end fraction end style

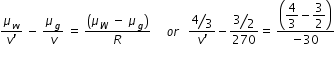...................(2)

from eqn.(2), we get v' = 120 cm

Hence second image is formed at 120 cm right side of lens, which is 40 cm behind the plane mirror.

Hence this image is virtual object of mirror and real image (third image) is formed 40 cm in front of mirror.

Now this third image acts as real object to spherical surface of water-glass interface

then we have,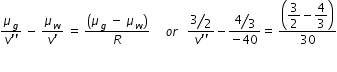

begin mathsize 12px style fraction numerator mu subscript g over denominator v apostrophe apostrophe end fraction space minus space fraction numerator mu subscript w over denominator v apostrophe end fraction space equals space fraction numerator open parentheses mu subscript g space minus space mu subscript w close parentheses over denominator R end fraction space space space space space o r space space space fraction numerator begin display style bevelled 3 over 2 end style over denominator v apostrophe apostrophe end fraction minus fraction numerator begin display style bevelled 4 over 3 end style over denominator negative 40 end fraction equals space fraction numerator open parentheses begin display style 3 over 2 end style minus begin display style 4 over 3 end style close parentheses over denominator 30 end fraction end style

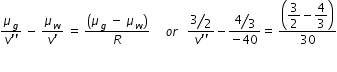..................(3)

from eqn.(3), we get v'' = -54 cm

Hence fourth image is formed at 54 cm at right side from lens.

Now finally applying same formula for spherical surface of glass-air surface,

begin mathsize 12px style 1 over v subscript f minus fraction numerator mu subscript g over denominator v apostrophe apostrophe end fraction space equals space fraction numerator open parentheses 1 minus mu subscript g close parentheses over denominator R end fraction space space o r space space 1 over v subscript f minus fraction numerator 1.5 over denominator negative 54 end fraction equals fraction numerator negative 0.5 over denominator negative 30 end fraction end style

.............................(4)

from eqn.(4), we get, v_f = -90 cm

Hence position of final image is 90 cm from lens at right side or 10 cm behind the mirror

Answered by Thiyagarajan K | 09 Jul, 2019, 10:19: AM

Application Videos