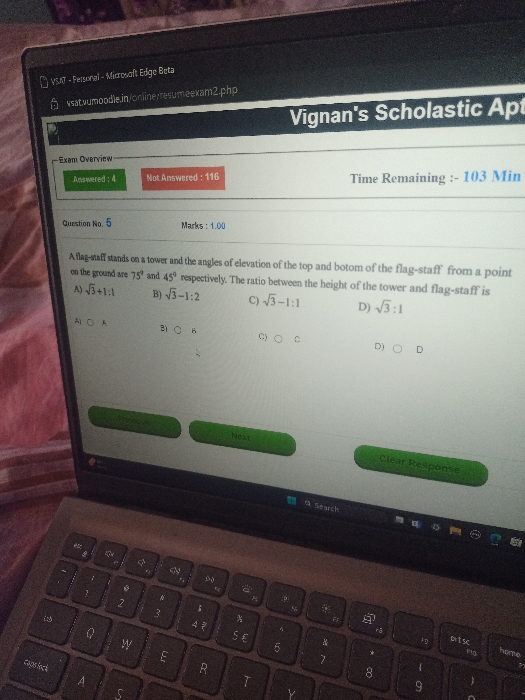
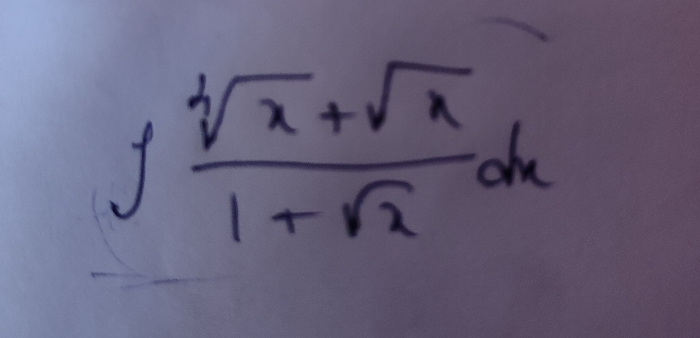CBSE Class 12-commerce Answered
Find the equation of the plane thrputh the line x-1/3= y-4/2 = z-4/-2 and parallel to the line x+1/2 = 1-y/4 = z+2/1. Hence find the shortest distance between the lines.
Asked by ponnarasan98 | 15 Mar, 2019, 07:27: PM
Equation of line passing through the plane is 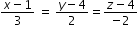 ..........................(1)
..........................(1)
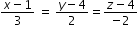 ..........................(1)
..........................(1)since the line passes through the point (1,4,4), this point lies in the plane.
Hence equation of the plane is a(x-1)+b(y-4)+c(z-4) = 0 ................................(2)
where a,b and c are direction ratios of the normal to the plane.
The plane is parallel to the line 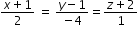 .........................(3)
.........................(3)
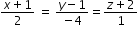 .........................(3)
.........................(3)Hence normal to the plane is perpendicular to dircetion of both the vectors associated to line (1) and (3).
Hence normal vector of the plane is obtained from cross product of vectors associated to line (1) and (3)
normal vector = 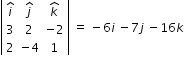
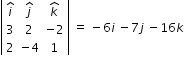
hence the direction ratios of normal are 6, 7, 16 . we get the equation of plane by substituting these direction ratios in eqn.(2)
a(x-1)+b(y-4)+c(z-4) = 6(x-1)+7(y-4)+16(z-4) = 6x+7y+16z-98 = 0 ............................(4)
The line given by eqn.(3) passes through the point (-1, 1, -2).
Hence distance between the lines is same as the perpendicular distance from this point to the plane given by eqn.(4)
Perpendicular distance from a point (x1 , y1 , z1 ) to the plane ax+by+cz-d=0 is 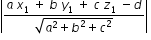
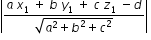
hence perpendicular distance = 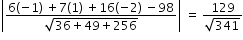
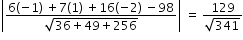
Answered by Thiyagarajan K | 16 Mar, 2019, 05:30: PM
Application Videos
Concept Videos
CBSE 12-commerce - Maths
Asked by hajarathvalishaik143 | 22 Apr, 2024, 11:32: AM
CBSE 12-commerce - Maths
Asked by nainaadityathakur | 02 Apr, 2024, 12:56: PM
CBSE 12-commerce - Maths
Asked by nainaadityathakur | 17 Mar, 2024, 03:04: PM
CBSE 12-commerce - Maths
Asked by morninggood0966 | 29 Feb, 2024, 04:06: PM
CBSE 12-commerce - Maths
Asked by manishpaladiya652 | 28 Feb, 2024, 11:26: AM
CBSE 12-commerce - Maths
Asked by pathvipatel144 | 25 Feb, 2024, 09:37: PM
CBSE 12-commerce - Maths
Asked by nainaadityathakur | 06 Feb, 2024, 01:38: PM
CBSE 12-commerce - Maths
Asked by najakatkhan6698 | 25 Dec, 2023, 10:37: AM
CBSE 12-commerce - Maths
Asked by mounikachitrala342 | 26 Oct, 2023, 07:59: AM
CBSE 12-commerce - Maths
Asked by darshanasharma0409 | 21 Sep, 2023, 06:07: PM